Pojem a řešení lineární nerovnice
- Lineární nerovnicí
-
s neznámou x nazveme každou nerovnici, kterou je možné ekvivalentními úpravami převést na jeden z těchto tvarů:
ax + b > 0 ax + b < 0 ax + b ≥ 0 ax + b ≤ 0 kde koeficienty a, b jsou libovolná reálná čísla.
Řešení lineárních nerovnic se velmi podobá řešení lineárních rovnic, jen s tím rozdílem, že nerovnice mívají obyčejně více kořenů. 
Při řešení nerovnic v oboru reálných čísel se málokdy stane, že by
nerovnice měla jen jeden kořen. Většinou jich má nekonečně mnoho, nebo žádný. Proto si před počítáním složitějších příkladů procvičíme jednoduché nerovnice, abychom natrénovali zápis různých množin kořenů.
Řešené příklady
-
Příklad 1
Řešte dané nerovnice v zadaném oboru řešení.
x ≥ − 4 v
-
Stejně jako u rovnic, i zde nejprve určíme O a D:
Na první pohled vidíme, že tuto nerovnici splňují všechna čísla, která jsou větší než − 4 a zároveň i číslo − 4. Tuto množinu zapíšeme jako polouzavřený interval reálných čísel od − 4 do
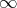. Tedy: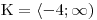
v -
Nenecháme se zmást tím, že x je na opačné straně nerovnice, než jsme zvyklí, a správně tuto nerovnost interpretujeme, jako: "x je menší než odmocnina ze tří". Tato nerovnice je opravdu jednoduchá, proto rovnou zapíšeme O, D i K.
-
x ≥ −4 v
-
Zdánlivě tato nerovnice vypadá jako ta první, kterou jsme řešili, ale rozdíl v O je tentokrát velmi podstatný. V oboru reálných čísel třeba tuto nerovnici splňuje číslo −1, jenže zde jej nemůžeme použít, protože to není číslo přirozené.
Na druhou stranu, uvědomíme-li si, co to jsou přirozená čísla
Přirozená čísla jsou kladná celá
čísla: 1, 2, 3, 4…, vidíme, že všechna tato čísla danou nerovnici splňují. Tedy:
-
x < 10 v
-
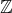
Opět si všimneme, že O nebude obor reálných čísel, a standardně začneme:
Tuto nerovnici budou řešit čísla jako: 9, 8, 7… . Ty však nemůžeme napsat pomocí intervalu
, protože tento interval obsahuje třeba i čísla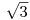 
a 2,5, která rozhodně nejsou celá.Bohužel navíc kořenů této nerovnice je nekonečně mnoho, a tak je do množiny K ani nemůžeme všechny vypsat. Budeme se tedy muset spokojit s neukončeným zápisem, kde nám tři tečky naznačí, že prvků v množině je nekonečně mnoho a že naznačená řada čísel pokračuje dále.
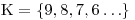
Což by se dalo zapsat i jako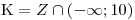 
.
Po těchto čtyřech příkladech bychom už měli mít jasno, kdy můžeme používat k zápisu
množiny K interval a kdy ne. Zároveň jsme si ukázali několik možností, jak se při zápisu
nekonečných množin bez intervalů obejít. Nejsou zde ale všechny možnosti, protože jich je příliš
mnoho, ale určitě se s nimi ještě setkáme v dalších příkladech.
Nyní si ukážeme řešení složitější nerovnice.
-
Příklad 2
Řešte v
nerovnici 
. -
Řešení
Pomocí dvou ekvivalentních úprav separujeme neznámou na levé straně nerovnice.
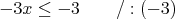
Výslednou nerovnici vydělíme koeficientem u x, tedy číslem-3. Nesmíme zapomenout, že tato úprava způsobí otočení znaménka nerovnosti.
Zapíšeme K. Nerovnici řešíme v oboru reálných čísel, proto můžeme použít k zápisu interval:
K =
Tento příklad nám jasně ukázal, že jednoduché lineární nerovnice se řeší obdobně jako rovnice.
Liší se většinou zápisem K a otáčením znaménka nerovnosti při dělení (násobení) celé nerovnice
záporným číslem.
Poslední příklad je věnován řešení jednoho speciálního typu lineárních nerovnic.
-
Příklad 3
Řešte v
nerovnici 
. -
Řešení
Nerovnici upravíme
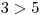
To, co jsme dostali po úpravě nerovnice, je nepravdivá nerovnost. Díváme-li se na tento výraz jako na nerovnost s proměnnou x, zjišťujeme, že ať už x nabude jakékoliv hodnoty, pravdivost této nerovnosti se nezmění. Bude tedy stále nepravdivá. Proto žádná hodnota x tuto nerovnici nesplňuje a tak:
Kdyby nám na konci vyšla nerovnost opačná, tedy 3 < 5, řešily by naopak tuto nerovnici
všechny možné hodnoty x. Pak by K = D =. Interpretace řešení původní nerovnice na základě nerovnosti 3 > 5 je obdobná jako u rovnice
v Úloze 2, kdy jsme dospěli k rovnosti 6 = −4. I u nerovnic je třeba ke správnému výsledku
provést úvahu, jak závisí platnost nerovnosti na hodnotě x, a teprve pak zapsat množinu K.