Co jsou kubické rovnice
- Kubickou rovnicí
-
nazveme každou rovnici, která se dá ekvivalentními úpravami převést na tvar ax3 + bx2 + cx + d = 0, kde x je neznámá, koeficienty a, b, c, d
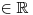a a ≠ 0.Obdobně jako u rovnic kvadratických pak ax3 nazveme kubický člen, bx2 nazveme kvadratický člen, cx lineární člen a d absolutní člen kubického čtyřčlenu.
Číslo a pak nazveme koeficient u kubického členu, b koeficient u kvadratického členu a číslo c koeficient u lineárního členu.
Každá kubická rovnice s reálnými koeficienty má minimálně jeden reálný kořen. Není ale úplně jednoduché se k tomuto kořeni dostat. Ačkoliv obdobně jako u kvadratické rovnice existují vzorce pro výpočet kořenů kubické rovnice, jejich výpočet je poměrně složitá záležitost. 
Často nám výsledky, které jsou jednoduchá přirozená čísla, poskytnou v tvaru plném odmocnin z komplexních čísel.
Ukážeme si proto nejprve tři postupy, jak můžeme vyřešit některé speciální kubické rovnice za pomoci znalostí, které již máme z předchozích kapitol, a na tyto vzorce jen odkážeme.
Kubické rovnice v součinovém tvaru
Máme-li kubickou rovnici zadanou v tzv. součinovém tvaru lineárních činitelů je určení jejích kořenů velmi jednoduché.
Kubická rovnice v součinovém tvaru vypadá následovně:
a(x − x1)(x − x2)(x − x3) = 0, kde x je neznámá a a, x1, x2, x3 jsou reálná čísla. Všimněte si, že tento tvar se velmi podobá rozkladu
kvadratického trojčlenu na součin pomocí Vietových vozrců.
Kořeny této rovnice pak jsou čísla x1, x2 a x3.
Kromě součinového tvaru, ještě můžeme snadno určit kořeny z částečného rozložení kubického čtyřčlenu na součin. Dostaneme-li kubickou rovnici zadánu ve tvaru: a(bx + c)(dx2 +ex + f) = 0, kde x je neznámá a a, b, c, d, e, f jsou reálná čísla, výpočet kořenů také nebude složitý.
Vyjdeme z tvrzení, že součin dvou výrazů je nulový, když alespoň jeden z těchto výrazů je nulový. Má-li součin lineárního dvojčlenu s kvadratickým trojčlenem být nulový Koeficient a nehraje při určování
nulovosti součinu roli, pokud a ≠ 0., musí být nulový alespoň jeden z nich, neboli kubickou rovci rozdělíme na řešení jedné lineární (bx + c = 0) a jedné kvadratické (dx2 +ex + f = 0) rovnice.
Lineární rovnice bx + c = 0 bude mít vždy jeden reálný kořen. Koeficient b totiž nesmí být nulový, jinak by původní zadání nebylo zadání kubické rce, ale jen kvadratické. A to je právě ten jeden reálný kořen, který musí mít každá kubická rovnice. Budeme-li totiž v návaznosti řešit kvadratickou rovnici dx2 +ex + f = 0, může se nám stát, že nebude mít v oboru reálných čísel kořeny.
-
Příklad 1
Řešte v
rovnici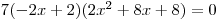 
.
-
Řešení
V zadání jsme opravdu dostali kubickou rovnici. Kdybychom totiž roznásobili závorky na levé straně rovnice, dostali bychom rovnici
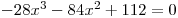. To ale dělat nebudeme, proto standardně nejprve určíme O a D. Výrazy v zadání jsou definované pro všechna reálná čísla, a tak 
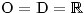.Má-li být součin nulový, musí být alespoň jeden činitel nulový. Proto řešení rozdělíme na dvě rovnice.
Nejprve vyřešíme rovnici
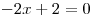, to je jednoduchá lineární rovnice a neměla by nám dělat problémy.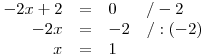
Vyřešíme i druhou rovnici
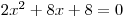, třeba pomocí vzorečku s diskriminantem.
Získali jsme tedy dva kořeny kubické rovnice −2
Kořen −2 je vlastně dvojnásobným kořenem,
takže bychom mohli říct, že máme tři kořeny. a 1 a můžeme zapsat K.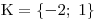
Takto bychom mohli dojít ke kořenům jakékoliv algebraické rovnice, kdyby byla zadána
jako součin lineárních a kvadratických členů.
Kubické rovnice bez absolutního členu
Dostaneme-li v zadání kubickou rovnici, která nemá absolutní člen, bude vypadat takto: ax3 + bx2 + cx = 0, kde x je neznámá, a, b, c jsou koeficienty z oboru reálných čísel a a ≠ 0.
Jak je vidět, z výrazu na levé straně rovnice můžeme jednoduše vytknout x a celou rovnici tak převedeme na předchozí případ, kdy máme rovnici zadanou jako součin lineárního a kvadratického členu.
-
Příklad 2
Řešte v
rovnici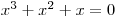 
.
-
Řešení
Nejprve určíme
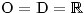.Z výrazu na pravé straně rovnice vytkneme x:
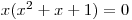
Řešení teď rozdělíme na řešení dvou rovnic:
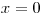a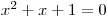 
.První rovnice je rovnou vyřešená a kořeny druhé určíme vzorečkem:
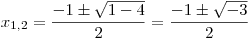
Ve vzorečku nám ale pod odmocninou vyšlo záporné číslo, diskriminant rovnice
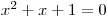je záporný, a ta proto nemá žádné reálné kořeny.Kubická rovnice ze zadání pak má pouze jeden reálný kořen, a to 0.
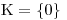
Každá kubická rovnice bez absolutního členu má kořen 0. Některé pak mají i další reálné kořeny.
Kubické rovnice s celočíselným kořenem
Víme-li, že daná kubická rovnice má celočíselný kořen, můžeme ho zkusit uhádnout. Pokud bychom totiž hodnotu takového kořenu znali, mohli bychom z kubického čtyřčlenu vytknout výraz x − k, kde k by byla hodnota známého kořenu. Tím kubický čtyřčlen převedeme na součin lineárního a kvadratického členu, což už umíme řešit.
Nalézt tuto hodnotu ale nemusí být vždy úplně jednoduché a nelze postupně dosazovat všechna celá čísla. Pokud ale kubickou rovnici upravíme na tvar x3 + px2 + qx + r = 0 Takovému tvaru se říká normovaný tvar rovnice., kde x je neznámá, p, q, r jsou koeficienty z oboru celých čísel, pak platí, že kořen k dělí bezezbytku koeficient r. Důkaz a další rozvinutí teorie najdete například v Calda [1]. V této publikaci dokonce najdete i kompletní teorii
o řešení algebraických rovnic s racionálními koeficienty
a racionálními kořeny.
-
Příklad 3
Řešte v
rovnici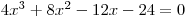 
o které víte, že má celočíselný kořen.
-
Řešení
Nejprve rovnici upravíme do tvaru, aby u kubického členu byl koeficient 1. Takže obě strany vydělíme 4.
Dostaneme rovnici
.Víme, že rovnice má celočíselný kořen. To znamená, že tento kořen musí dělit číslo −6. Dělitelé −6 jsou tito:
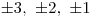, takže kořen bude jeden z těchto čísel.Postupně je budeme dosazovat do rovnice a zkoušet, který z nich to je. Nakonec zjistíme, že kořenem je číslo −2.
Známe-li kořen −2, vydělíme kubický čtyřčlen lineárním výrazem x + 2.
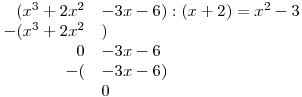
Takže kubický výraz na levé straně rovnice se dá nahradit součinem:
.Zbývá vypočítat, zda existují, a jaké jsou zbývající kořeny. Na první pohled je ale vidět, že to budou čísla
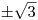
Nevidíte-li to, stačí jakoukoliv metodou vypočítat kořeny rce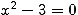 
.. Teď už zbývá určit K.
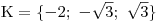
Většina, ale nikoliv všechny, kubické rovnice, se kterými se setkáte ve středoškolských učebnicích
a sbírkách, má jeden celočíselný kořen. Bohužel některé rovnice se nedají upravit do tvaru
s koeficientem 1 u kubického členu a celočíselným absolutním členem, a proto se občas vyplatí
zkusit tento kořen "uhádnout" vyzkoušením čísel −2, −1, 1, 2 apod.
Obecná kubická rovnice
Pokud bychom měli řešit kubickou rovnici, která nespadá do případů uvedených výše, nezbylo by nám už nic jiného, než použít Cardanovy vzorce. Jejich odvození ale není jednoduché, vyžaduje znalosti z teorie komplexních čísel a i značný matematický nadhled.
Proto zde najdete jen odkazy na stránky, které se této problematice do hloubky věnují.
Povídání o kubických rovnicích a Cardanových vzorcích najdete na české Wikipedii, pro řešitele Korespondenčního semináře KAM MFF UK vznikl tento materiál od Petra Šimečka. Zcela vyčerpávající pojednání o řešení kubických rovnic, které je ale určeno spíše studentů vysokých škol, najdete zde. Autora poslední práce se bohužel nepodařilo určit.