Pojem iracionální rovnice
Iracionální rovnice se nazývají rovnice s neznámou pod odmocninou. Na střední škole se nepotkáme s jinými odmocninami než s druhými, ale řešení rovnic s odmocninami vyšších řádů je velmi obdobné. Základní ekvivalentní úpravou, kterou budeme v této kapitole používat je umocnění obou stran rovnice na druhou.
Tato úprava je ekvivalentní pouze, když obě strany rovnice mají stejné znaménko. Pokud ale toto nebudeme u řešených rovnic schopni zajistit a použijeme-li přesto tuto úpravu, může se stát, že získáme rovnici, která už nebude ekvivalentní s původní. 
Taková úprava rovnice se pak nazývá
důsledková úprava rovnice.
Více o nich se o nich zmiňuje Polák [8]. Kořeny původní rovnice budou kořeny i nadále, ale je možné, že rovnice, kterou získáme po umocnění bude mít ještě nějaké kořeny navíc. Bude tedy nezbytně nutné, abychom po jejich vypočtení, provedli zkoušku, kterou si správnost vypočtených hodnot ověříme.
Po umocnění rovnice se nám podaří buď odmocnin úplně zbavit a dostaneme např. lineární, či kvadratickou rovnici, nebo nám nějaké neznámé pod odmocninami zůstanou a budeme umocňováním řešit další iracionální rovnici.
Nezapomeňte, že druhá odmocnina je definovaná jen pro nezáporná reálná čísla. Pokud se tedy pod odmocninou vyskytuje výraz s neznámou x, výrazně to ovlivní definiční obor rovnice.
Řešené příklady
-
Příklad 1
Řešte v
rovnici 
. -
Řešení
Nejprve určíme O a D.
Nesmíme zapomenout, že výraz pod odmocninou musí být nezáporný. Vyřešíme tedy jednoduchou lineární nerovnici a zapíšeme O a D.
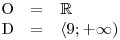
Výrazy na obou stranách rovnice jsou nezáporné
Číslo 4 je evidentně kladné. Stejně tak výraz na
levé straně rovnice, protože druhá odmocnina
"vrací" pouze nezáporná čísla., a tak můžeme výrazy na obou stranách rovnice umocnit na druhou.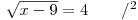
Umocnit číslo na pravé straně je jednoduché, ale výraz na straně levé by někomu mohl dělat potíže. Není to ale nic těžkého. Po umocnění druhé odmocniny z libovolného výrazu na druhou dostaneme daný výraz:
.
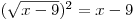Vyšel nám kořen 25. Jelikož jsme k němu došli pouze ekvivalentními úpravami
Při umocňování celé rce byly obě strany nezáporné., můžeme zapsat množinu K.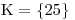
Většina iracionálních rovnic s jednou odmocninou se dá jednoduše vyřešit jedním umocněním obou
stran rce. Je třeba si před umocňováním zajistit, aby odmocnina byla sama na jedné straně rce
a ostatní výrazy na straně opačné.
Pokud rovnice obsahuje více odmocnin a výrazy na obou stranách jsou složitější, může se samozřejmě i zkomplikovat řešení takového příkladu.
-
Příklad 2
Řešte v
rovnici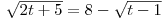 
. -
Řešení
Nejprve určíme O a D.
Z výrazů pod odmocninou získáme podmínky, které vymezí definiční obor.
Podíváme-li se na rovnici, zjistíme, že výraz na pravé straně rovnice nebude mít stejné znaménko pro všechny hodnoty t z D. Např. pro hodnotu t = 101, bude záporný, zatímco pro hodnotu t = 2 bude kladný. Přesto použijeme úpravu umocnění obou stran rovnice
...jinak se totiž zbavit odmocnin neumíme
a z tohoto zadání nedokážeme řešení uhádnout., ale musíme si zapamatovat, že na závěr provedeme zkoušku, zda jsme umocněním nepřidali nějaké další kořeny.
Všimněte si umocnění pravé strany rce. Celý výraz na pravé
straně totiž umocňujeme podle vzorečku (a − b)2.Je vidět, že jedno umocnění obou stran rovnice nám ještě nepomohlo se zbavit odmocnin. Budeme muset tuto úpravu zopakovat. Před tím je ale nutné si převést výrazy bez odmocniny na jednu stranu rovnice a samotnou odmocninu nechat na druhé straně.
Při prvním umocňování jsme prováděli důsledkovou úpravu,
a tak nyní už nemusíme ověřovat nezápornost obou stran rovnice,
protože zkoušku už musíme stejně dělat.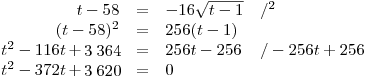
Dostali jsme kvadratickou rovnici, která sice nemá "nejhezčí" koeficienty, ale přesto půjde jednoduše vyřešit pomocí vzorečku s diskriminantem:
Vyšly nám dvě hodnoty: 10 a 362. Než ale zapíšeme K, musíme provést zkoušku.
Zkouška nám ukázala, že číslo 10 je kořenem i původně zadané rovnice.
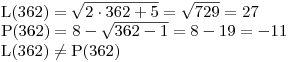
Zkouška pro t = 362 ale ukázala, že toto číslo není kořenem původní rovnice. Je to jen zdánlivý kořen, který se objevil proto, že jsme neprováděli pouze ekvivalentní úpravy. Proto:
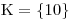
Stačí abychom jednou použili důsledkovou úpravu rce a je nutné dělat zkoušku. Proto u druhého
umocňování obou stran rce jsme si odpustili určování znamének výrazů na obou stranách rce.