Úlohy k opakování
-
Úloha 1
Řešte zpaměti v
 rovnici
rovnici 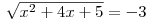 .
. -
 Jaké znaménko mají obě strany rce?
Jaké znaménko mají obě strany rce?
Výraz pod odmocninou je pro všechna
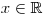 vždy kladný, proto
vždy kladný, proto 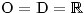 .
.Levá strana rce nabývá vždy nezáporných hodnot, zatímco pravá je vždy záporná.
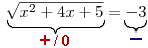
Tato rovnost nemůže být nikdy naplněna, a proto
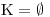 .
.

-
Úloha 2
Řešte v
 rovnici
rovnici 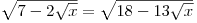 .
. -
 Určíme O a D.
Určíme O a D.
V zadání úlohy jsou celkem čtyři odmocniny, které v sobě obsahují výraz s neznámou. Musíme tedy určit, jakých hodnot může x nabývat, aby všechny byly definované. Dvě odmocniny obsahují jen x, proto nám bude stačit řešit jen tři nerce a na závěr uděláme jejich konjunkci.
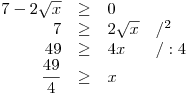
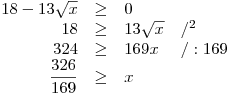
x > 0
Určíme konjunkci podmínek:
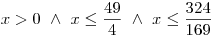
Toto je splněno, pokud
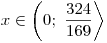 .
.Nyní už můžeme zapsat O a D.
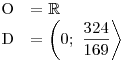
 Když už známe definiční obor, můžeme začít řešit rci umocněním obou stran.
Když už známe definiční obor, můžeme začít řešit rci umocněním obou stran.
Řešenou rci postupně upravujeme, protože se prvním umocněním nezbavíme všech odmocnin, provedeme ještě druhé. Předtím ale v rci osamostatníme výraz s odmocninou na jedné její straně.
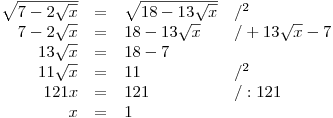
 Určíme K.
Určíme K.
Rovnici sice řešíme pro
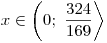 , vypočtená hodnota x do tohoto intervalu ale patří a tak ji můžeme zařadit do K.
, vypočtená hodnota x do tohoto intervalu ale patří a tak ji můžeme zařadit do K.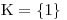
 Ačkoliv to výše ve výpočtu nebylo nikde explicitně zmíněno, při každém
Ačkoliv to výše ve výpočtu nebylo nikde explicitně zmíněno, při každém
umocňování obou stran rce (či nerce při určování podmínek),
jsme si pečlivě hlídali, aby obě strany rce byly vždy nezáporné!

-
Úloha 3
Řešte v
 nerovnici
nerovnici 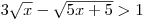 .
. -
 Určíme O a D.
Určíme O a D.
Zadání nerce obsahuje dvě odmocniny s výrazy s neznámou pod nimi. Vyřešíme soustavu dvou nerovnic s jednou neznámou, abychom získali podmínky pro platnost těchto výrazů.
x > 0
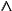
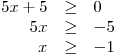
Konjunkcí podmínek získáváme
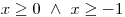 . Nyní už snadno zapíšeme O a D.
. Nyní už snadno zapíšeme O a D.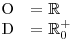
 Upravíme nerci a umocníme ji.
Upravíme nerci a umocníme ji.
Nerovnici před umocněním upravíme tak, abychom na obou stranách měli nezáporné výrazy.
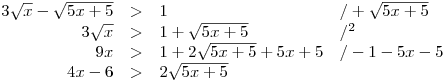
 Než nerovnici podruhé umocníme, určíme znaménka obou stran.
Než nerovnici podruhé umocníme, určíme znaménka obou stran.
Zatímco pravá strana nerovnice je vždy nezáporná, levá své znaménko mění podle hodnoty x. Rozdělíme tedy další řešení do dvou větví. Nejprve si ale určíme, pro která x bude levá strana nezáporná.
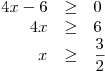
Nyní rozdělíme řešení do dvou větví:
Pro 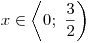
 Nezapomeňte, že definiční obor jsou "jen"
Nezapomeňte, že definiční obor jsou "jen" 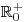 ,
,
proto x nemůže nabývat záporných hodnot.Pro 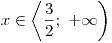
 Vyřešíme první větev nerce?
Vyřešíme první větev nerce?
Levá strana nerce je tedy vždy záporná, zatímco pravá je vždy kladná.
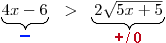
Požadovaná nerovnost tedy není nikdy splněna a
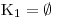 .
. Vyřešíme druhou větev nerce?
Vyřešíme druhou větev nerce?
Obě strany nerce jsou nezáporné a tak je můžeme umocnit.
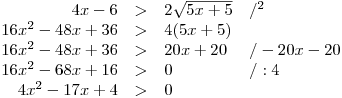
 Vyřešíme kvadratickou nerci grafickou metodou.
Vyřešíme kvadratickou nerci grafickou metodou.
Vypočteme kořeny příslušné kvadratické rce.
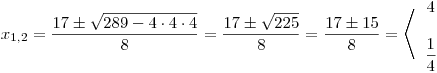
Načrtneme graf příslušné kvadratické funkce a vyznačíme x, která splňují nerovnost.
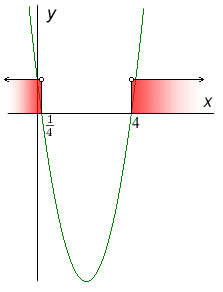
 Určíme K2.
Určíme K2.
Podle grafu řeší nerci 4x2 − 17x + 4 > 0 všechna
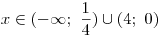
Nesmíme ale zapomenout na omezení hodnot x dané touto větví řešení, které nám říká, že
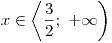 .
.
Určíme tedy množinu všech řešení v této větvi nerce takto:
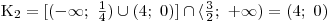
 Určíme výsledné K.
Určíme výsledné K.
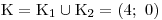
 Tento težší příklad iracionální nerce dobře ilustruje všechny potřebné znalosti a dovednosti,
Tento težší příklad iracionální nerce dobře ilustruje všechny potřebné znalosti a dovednosti,
které byste si měli z této kapitoly odnést. Pokud si některým krokem nejste jisti, nechápete ho,
zkuste si znovu prostudovat příslušnou teorii v předchozích kapitolách,
nebo využijte doporučenou literaturu, kde najdete další výklad a vzorová řešení.

Testíky
Klikněte na otazník u odpovědi, o které myslíte, že je dobře, a smajlík vám prozradí, zda jste odpověděli správně. U každého příkladu je jen jedna správná možnost.
|
Určete D pro rovnici
|
Určete D pro rovnici
|
|
Určete D pro rovnici
|
Určete D pro nerovnici
|
Řešení dalších úloh si můžete vyzkoušet v testu za kapitolou rovnice vyšších řádů.

