ROVNICE
A NEROVNICE

Kvadratické rovnice

Co to jsou kvadratické rovnice

Kvadratickým trojčlenem

nazveme každý výraz ve tvaru ax2 + bx + c, kde x je proměnná, a, b, c 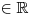jsou koeficienty z oboru reálných čísel a a ≠ 0.

Člen ax2 nazveme kvadratický člen, bx lineární člen a c absolutní člen kvadratického trojčlenu. Číslo a pak nazveme koeficient u kvadratického členu a číslo b koeficient u lineárního členu.

Kvadratickou rovnicí

nazveme každou rovnici, která se dá ekvivalentními úpravami převést na tvar ax2 + bx + c = 0, kde x je neznámá, a, b, c jsou koeficienty z oboru reálných čísel a a ≠ 0.

Tento tvar kvadratické rovnice budeme dále v této práci nazývat základním tvarem kvadratické rovnice.

Podmínka o nenulovosti koeficientu a je nezbytná, neboť bychom jinak pracovali s lineárními rovnicemi, pro které platí trošku jiné zákonitosti a pro jejichž řešení se používají jiné postupy.

Dle zadání je vidět, že stejně jako lineární rovnice, tak základní tvar kvadratické rovnice neobsahuje žádné nedefinované výrazy pro všechna reálná čísla. Definiční obor D těchto "základních" rovnic tedy bude stejný jako obor řešení O. nahoru

Řešení kvadratických rovnic

Budeme-li řešit kvadratické rovnice v oboru reálných čísel, brzy zjistíme, že některé rovnice nebudou mít kořen. Jiné kvadratické rovnice budou mít kořen jen jeden a ostatní kvadratické rovnice budou mít kořeny právě dva. Kdy tyto případy nastanou a jak je rozlišit, si ukážeme dále.

Oproti řešení lineárních rovnic budeme skoro všechny kvadratické rovnice, které budeme kdy řešit, upravovat do základního tvaru. Budeme totiž potřebovat znát koeficienty a, b a c. Pro řešení kvadratických rovnic existuje vzoreček, pomocí kterého vypočítáme případné kořeny každé rovnice, pokud tato rovnice reálné kořeny má. Vzorec si musíte zapamatovat velmi pečlivě. Řešení kvadratických rovnic se ve středoškolské matematice vyskytuje v různých tématech, a proto se vám bude hodit i v budoucnu.

Pro výpočet kořenů x1 a x2kvadratické rovnice ax2 + bx + c = 0 platí tyto vzorce:

a ,

které se zpravidla spojují do jednoho vzorečku

. Důkaz platnosti tohoto vzorečku je založen na doplnění kvadratického
trojčlenu "na čtverec" a můžete jej nalézt v učebnici Charvát a kol. [3].

Nejzajímavější část vzorečku je výraz . Druhá odmocnina je definovaná jen pro nezáporná reálná čísla, ale může obecně nabývat i záporných hodnot. Což v konečném důsledku znamená, že daná kvadratická rovnice nemá reálné kořeny.

Zároveň, když se podíváme na vzorečky pro kořeny x1 a x2, můžete si všimnout, že se liší jen znaménkem před odmocninou. Vyjde-li nám výraz nulový, bude nulová i jeho odmocnina; pak nám vzorečky pro kořeny x1 a x2 poskytnou stejné výsledky a vyjde nám jen jeden kořen.

Jak je vidět, na hodnotě hodně záleží, proto ji trochu vyzdvihneme.

Diskriminantem kvadratické rovnice ax2 + bx + c = 0 nazveme hodnotu a označíme ji D.

nahoru

Shrnutí postupu řešení kvadratických rovnic

  1. Určíme O a D rovnice.
  2. Upravíme kvadratickou rovnici na základní tvar ax2 + bx + c = 0, určíme a, b, c.
  3. Vypočteme diskriminant D = b2 − 4ac.Nepleťte si diskriminant značený D a definiční obor rce D.
  4. Podle hodnoty D určíme počet a hodnotu případných kořenů rovnice:
    1. Pro D < 0 pak kvadratická rovnice nemá reálné kořeny.
    2. Pro D = 0 pak kvadratická rovnice má jeden reálný kořen .
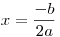      Tento kořen se také někdy nazývá dvojnásobný kořen.
    3. Pro D > 0 pak kvadratická rovnice má dva různé reálné kořeny,
      které určíme ze vzorečku .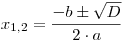
  5. Zapíšeme K rovnice.
Pokud si tento postup nechcete pamatovat, nemusíte. Někdy také stačí prostě dosadit hodnoty
koeficientů a,b,c do vzorečku a počítat. Musíte jen vědět, co dělat, když vám
pod odmocninou vyjde nula, nebo záporné číslo. nahoru

Metody řešení kvadratických rovnic ve speciálním tvaru

Jak už bylo uvedeno, výpočet kořenů kvadratické rovnice pomocí vzorečku s diskriminantem je univerzální metoda fungující vždy, pro všechny kvadratické rovnice. Někdy se ale vyplatí znát i jiné metody řešení, zejména proto, že jsou rychlejší pro výpočet. Obecně se dají alternativními metodami počítat kvadratické rovnice, které mají buď koeficient b, nebo koeficient c nulový.

Kvadratická rovnice bez absolutního členu

To je rovnice, v níž je c = 0, neboli má tvar ax2 + bx = 0. Dá se řešit vytknutím x z výrazu na levé straně rovnice a úvahou o nulovosti součinu.

Příklad 1

Řešte v rovnici 2x2 + x = 0.

O = D =

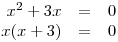
Součin je nulový, právě když je alespoň jeden z činitelů nulový, neboli .

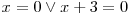Proto x1= 0 a x2= −3, a tedy K={−3; 0}.

nahoru

Kvadratická rovnice bez lineárního členu

To je rovnice, v níž je b = 0, neboli má tvar ax2 + c = 0. Dá se řešit osamostatněním x2 na levé straně rovnice a následným "odmocněním obou stran rovnice".

Příklad 2

Řešte v rovnici 2x2 − 8 = 0.

O = D =

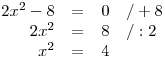
Protože obě strany rovnice jsou kladné, můžeme je obě odmocnit Pozor, odmocňování obou stran rce obecně není ekvivalentní úprava.
Pouze v případě, jako je zde popsáno. a dostaneme:

| x | = 2 .

A tuto rovnici už dořešíme jednoduše. Hned nás napadne kořen 2, ale mělo by nás napadnout, že tuto rovnici řeší i kořen −2.

Proto x1= 2 a x2= −2, a tedy K={−2; 2}.

Opravdu ale není nezbytné si toto pamatovat, protože vzoreček
s diskriminantem funguje i na tyto typy kvadratických rovnic. nahoru

Řešené příklady

Příklad 3

Řešte v rovnici .

Nejprve standardně určíme O = D = .

V prvních příkladech ještě budeme určovat hodnotu koeficientů a,b,c, abychom získali jistotu při dalším počítání ve vzorečcích.

a = 9; b = 12; c = 4

Vypočteme diskriminant 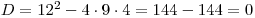. Kvůli nulovému diskriminantu víme, že rovnice bude mít jen jeden kořen. Ten získáme dosazením do vzorečku: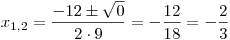

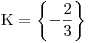
nahoru

Příklad 4

Řešte v rovnici .

Opět určíme O = D = .

Určíme hodnotu koeficientů a,b,c:

a = 1; b = 1; c = 1

Vypočteme diskriminant 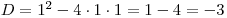. Ten nám tentokrát vyšel záporný, a tak rovnou zapíšeme .

nahoru

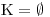Příklad 5

Řešte v rovnici .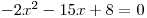

O = D =

Určíme hodnotu koeficientů a,b,c:

a = −2; b = −15; c = 8

Diskriminant 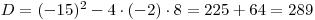tentokrát vyšel kladný, a proto dosazením do vzorečku dopočítáme dva kořeny: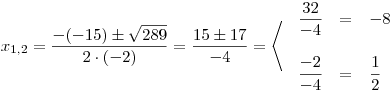

A určíme .

Ukázali jsme si řešení tří základních druhů kvadratických rovnic. Jak je vidět, pokud známe vzoreček,
nic těžkého na tom není. Takže jediné problémy by mohly nastat při úpravě rce na základní tvar
nebo při hledání řešení v jiném O než .

nahoru

Někdy nebude úplně jednoduché se k základnímu tvaru kvadratické nerovnice dostat a kořeny nebudou celočíselné.

Příklad 6

Řešte v rovnici .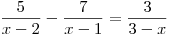

Řešení

Nejprve standardně určíme O a D. V zadání rovnice se ale vyskytují tři zlomky, které mají ve jmenovateli jednoduché lineární výrazy. Musíme tedy jejich nulové body vyřadit z definičního oboru. Proto:

Nyní začneme upravovat rovnici tak, abychom získali základní tvar. Nejprve celou rovnici vynásobíme všemi třemi lineárními výrazy z jmenovatelů, abychom se zbavili zlomků.

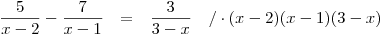
Teď budeme výrazy na obou stranách upravovat a na závěr vše převedeme na levou stranu rovnice.

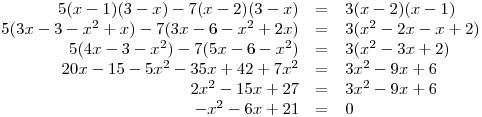
Určíme hodnotu koeficientů a,b,c, a dosazením do vzorečku vypočteme kořeny.

a = −1; b = −6; c = 21

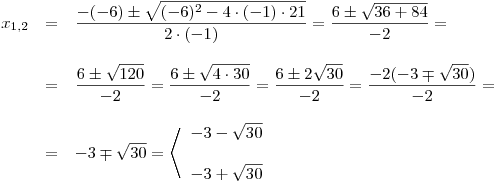
Všimněte si vytknutí −2 z čitatele ve druhém řádku. Sice jsme před odmocninou místo ±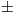
po vytknutí použili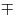 , ale jediné na čem se to projevilo bylo pořadí kořenů.
Proto se to v běžném zápisu řešení nedělá.

Zapíšeme K:

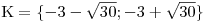
Odmocnina z 30 se už nedá částečně odmocnit. Navíc je to
iracionální číslo, které nejde přesně vyčíslit, a proto ji nebudeme dále
upravovat a necháme ji ve vyjádření výsledku tak, jak je uvedeno.

Z jednoduchého zadání se nakonec vyklubal příklad, který nás pěkně potrápil nejen při úpravách
rce, ale i při částečném odmocňování, vytýkání a krácení. To jsou ale dovednosti, které musíme
stále v matematice ovládat při jakémkoliv tématu.

nahoru

Kvadratické rovnice v oboru komplexních čísel

Řešíme-li kvadratické rovnice v oboru komplexních čísel, můžeme postupovat obdobně jako při řešení v oboru reálných čísel. V oboru komplexních čísel máme navíc definovánu i odmocninu ze záporného reálného čísla, proto bude mít každá kvadratická rovnice alespoň jeden kořen. Někdy se setkáte i s tvrzením, že v komplexním oboru řešení má kvadratická rce právě dva kořeny.
Záleží to na náhledu na tzv. dvojnásobný kořen (když D = 0), jestli jej bereme jako jeden kořen, nebo
jako dva kořeny o stejné hodnotě.

Více o této problematice se můžete dočíst v diplomové práci Lenky Svobodové (Šilarové) věnované právě komplexním číslům.

nahoru