Úvod Úvod a ovládání Řešení rovnic a nerovnic Lineární rovnice Lineární nerovnice  Test 1 – lineární Kvadratické rovnice Kvadratické nerovnice  Test 2 – kvadratické Iracionální rce a nerce Parametry a abs. hodn. Rovnice vyšších řádů  Test 3 Soustavy rovnic  Test 4 – soustavy Odkazy a literatura
Přehled stránek

Základní pojmy

S pojmem rovnice jsme se již určitě setkali. Připomeneme si tento pojem několika ukázkami.

2x - 3 = 5 je příkladem rovnice s neznámou x.

2x² - 3y = 5 + y³ je příkladem rovnice s dvěma neznámými x a y.

Obdobně jako rovnici, připomeneme si na příkladu i nerovnici. V nerovnici místo znaménka pro rovnost použijeme znaménko pro větší (větší nebo rovno, menší, menší nebo rovno).

5x + 3 > 5 je příkladem nerovnice s neznámou x.

  x² ≥ 5 + x
−5x < 5        je příkladem soustavy dvou nerovnic s jednou neznámou x.

Pro začátek budeme uvažovat, že dané výrazy na obou stranách rovnice (resp. nerovnice) budou obsahovat pouze jednu neznámou, a to x Samozřejmě je možné v rovnicích používat
místo x i jiná písmenka.. Pak výraz, který je na levé straně rovnosti (resp. znaménka větší apod.), označíme jako L(x) a nazveme ho levou stranou rovnice (nerovnice). Obdobně celý výraz vpravo od symbolu rovnítka (resp. znaménka větší apod.) označíme jako P(x) a nazveme ho pravá strana rovnice (nerovnice). Pro rce s jinou neznámou, např. t, označíme
levou stranu L(t) a pravou stranu rce P(t).

Hledáme-li pak řešení rovnice (nerovnice), hledáme vlastně všechny možné hodnoty neznámé x takové, aby po dosazení těchto hodnot do levé a pravé strany rovnice (nerovnice), byla splněna rovnost L(x) = P(x) (nerovnost L(x) > P(x) apod.). Tyto hodnoty neznámých pak nazveme kořeny dané rovnice (nerovnice). Někdy se místo spojení "kořeny rovnice (nerovnice)" používá termín řešení rovnice (nerovnice).
Toto spojení ale může vyjadřovat jak samotný postup, jeden z kořenů dané rovnice, tak i množinu
všech kořenů rovnice. Proto raději zůstaneme u pojmu kořen rovnice.

Množinu, ve které hledáme všechny kořeny rovnice, označíme O a nazveme ji oborem řešení rovnice. Množinu, která vznikne jako průnik množiny O a množin, ve kterých jsou definovány výrazy L(x) a P(x), označíme D a nazveme ji definiční obor rovnice. A množinu všech kořenů dané rovnice pak označíme písmenem K. Obdobnou terminologii pak používáme i u nerovnic. Velmi důležitý je i vztah mezi těmito množinami: K D O. Mělo by být zřejmé, že kořenem nemůže být číslo, které nepatří do definičního oboru. Tyto tři množiny budeme určovat u každého řešeného příkladu.

Úmluva

Není-li řečeno v zadání všech rovnic a nerovnic v této práci jinak, budeme všechny zde uvedené rovnice řešit v oboru reálných čísel, neboli O = .

Zároveň pro zjednodušení zápisu zadání budeme předpokládat, že vyskytuje-li se v zápisu rovnice jen jedno písmenko, je to ta neznámá, pro kterou máme danou rovnici řešit.

Příklad rovnice s neznámou x

Příklad nerovnice s neznámou s

Řešení rovnic

Už od pradávna se lidé pokouší rovnice řešit, více, či méně úspěšně. U většiny rovnic, o kterých se bude zmiňovat tato práce, existuje jednoznačný postup, který nám poskytne všechny kořeny dané rovnice. Ale to neznamená, že by některé rovnice nešlo řešit efektivněji jinými metodami, často založenými na logickém úsudku, nebo experimentálním dosazováním vybraných čísel za neznámou. My si ale prozradíme metody klasické, a to pomocí ekvivalentních úprav.

Ekvivalentní úpravy

Ekvivalentní rovnice

Dvě rovnice nazveme ekvivalentní, právě když mají stejnou množinu kořenů. Ekvivalentní jsou například rovnice:x = 2; 2x = 4
a x + 2 = 4 Všechny mají K = {2}.

Ekvivalentní úprava

Úpravu rovnice nazveme ekvivalentní úpravou, právě když tato úprava převede rovnici na rovnici jinou, s ní ekvivalentní.

Obojí se dá obdobně vztáhnout pro nerovnice.

Přehled ekvivalentních úprav rovnic

1. Vzájemná výměna stran rovnice.
2. Přičtení téhož čísla, nebo výrazu obsahující neznámou, který je definovaný v celém O, k oběma stranám rovnice. Protože odečtení nějakého čísla se dá zapsat jako přičtení opačné
   hodnoty tohoto čísla, stačí nám zde uvedená formulace i pro
   zavedení ekvivalentní úpravy odečtení čísla nebo výrazu
   od obou stran rce.
3. Vynásobení obou stran rovnice stejným číslem nebo výrazem s neznámou, který je definovaný a nenulový v celém O. Když si uvědomíme, že dělení nějakým číslem je vlastně jen násobení převrácenou hodnotou tohoto čísla,
   dostali jsme touto formulací i ekvivalentní úpravu pro dělení obou stran rovnice výrazem.
4. Umocnění obou stran rovnice přirozeným mocnitelem, jsou-li obě strany rovnice nezáporné (nebo naopak záporné) v celém oboru řešení rovnice O.

Ukázky ekvivalentních úprav rovnic

Animovaný příklad ukazuje situaci jednoduché lineární rovnice, kterou je třeba upravit tak, abychom všechny výrazy, které obsahují neznámou, dostali na jednu stranu rovnice, a výrazy bez neznámé na stranu opačnou. K tomu právě vhodně využíváme ekvivalentní úpravy přičítání a odčítání čísel, či výrazů.

Druhý příklad ukazuje výhodnost ekvivalentní úpravy násobení obou stran rovnice nenulovým číslem. Pokud zvolíme správné číslo, můžeme se zbavit počítání se zlomky a celou rovnici převést na jinou, daleko jednodušeji zapsanou i řešitelnou.

Ekvivalentních úprav rovnic je více, ale nám v celém rozsahu práce budou tyto uvedené stačit. Zejména si budeme dávat pozor na čtvrtou zmíněnou ekvivalentní úpravu, abychom ji používali tak, jak se má. Pokud bychom umocnili strany rovnice, které mají opačná znaménka, mohli bychom do rovnice přidat "další kořen". Resp. by získanou rci řešily i další kořeny, které by nebyly kořeny původní rce. Pak by umocnění obou stran rovnice již nebylo ekvivalentní, ale důsledkovou (implikační) úpravou. Pokud si nebudete jisti, zda jste vždy používali pouze ekvivalentní úpravy, nebo zda jste neudělali chybu, je nejlepší provést zkoušku řešení.

Při provádění zkoušky dosadíme spočítané kořeny do výrazu na levé a pravé straně rovnice a spočítáme jejich hodnotu. Pokud tyto hodnoty nejsou stejné, pak nalezený kořen není skutečným kořenem rovnice. Nebo jsme někde udělali chybu. Samotné úpravy a zkoušku pak budeme trénovat v kapitole lineární rovnice. Zkouška u rovnic není v případě použití výhradně ekvivalentních úprav povinná, ale vyplatí se ji dělat, protože
nám potvrdí správnost vyřešení příkladu, či odhalí chybu.

Řešení nerovnic

Řešit nerovnice bývá o něco komplikovanější a obtížnější, než řešit podobné rovnice. Zejména proto, že nám vychází daleko více kořenů. Ty je potřeba umět správně zapisovat pomocí intervalů reálných čísel nebo pomocí značení číselných oborů. Další komplikace vyvstávají v tom, že při řešení nerovnic fungují trochu jiné ekvivalentní úpravy, než při řešení rovnic.

Přehled ekvivalentních úprav nerovnic

1. Vzájemná výměna stran nerovnice se současným otočením znaménka nerovnosti.
2. Přičtení téhož čísla, nebo výrazu obsahující neznámou, který je definován na celém O, k oběma stranám nerovnice.
3. Vynásobení obou stran nerovnice číslem, nebo výrazem s neznámou, který je definovaný a kladný Je-li číslo, nebo výraz kladný, je různý od nuly., pro všechny hodnoty neznámé z O.
4. Vynásobení obou stran nerovnice záporným číslem, nebo výrazem s neznámou, který je záporný a definovaný v celém O, přitom znak nerovnosti se mění v obrácený. Využitím stejných úvah, jako u ekvivalentních úprav rovnic, můžeme body 2, 3 a 4
   rozšířit na odčítání od obou stran nerce a dělení obou stran nerce nenulovým číslem, nebo nenulovým
   výrazem definovaným na O. Samozřejmě nezapomene otáčet znaménko nerovnosti, pokud by
   byl výraz, nebo číslo, kterým dělíme, záporný.
5. Umocnění obou stran nerovnice přirozeným mocnitelem, jsou-li obě strany nerovnice nezáporné v celém oboru řešení nerovnice O.
6. Umocnění obou stran nerovnice přirozeným mocnitelem, jsou-li obě strany nerovnice nekladné v celém O a současným otočením znaménka nerovnosti.

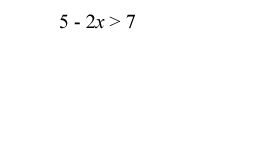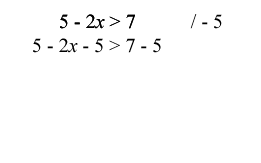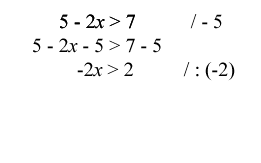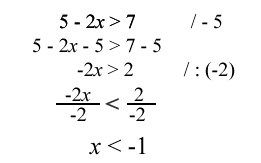V ukázce ekvivalentních úprav nerovnic jsou předvedeny dvě úpravy: odečítání čísla 5 od obou stran nerovnice a dělení rovnice −2. Zatímco u první operace zůstává znaménko nerovnosti neměnné, u dělení záporným číslem se znaménko nerovnosti musí otočit.

Samotné úpravy pak budeme procvičovat v kapitole věnované lineárním nerovnicím.

Řešení soustav rovnic

Pokaždé, když budeme řešit soustavu více rovnic s více neznámými, jde nám o nalezení takové kombinace hodnot všech neznámých, aby byli splněny všechny rovnice v soustavě zároveň. Tyto výsledky pak zapisujeme pomocí tzv. uspořádaných n-tic, kde n je počet neznámých, a které se zapisují pomocí hranatých závorek. Řešíme-li soustavu tří rovnic se třemi neznámými a vyjdou nám kořeny x = 1, y = 3, z= −2, zapíšeme tyto kořeny
do jedné uspořádané trojice tak, aby neznámé, které v soustavě figurovaly,
byly uspořádány podle abecedy vzestupně. Tedy: [1; 3; −2].

Přehled ekvivalentních úprav soustav rovnic

1. Nahrazení libovolné rovnice soustavy rovnicí, která je s původní rovnicí ekvivalentní (původní rovnici upravíme pomocí libovolné ekvivalentní úpravy pro řešení rovnic).
2. Nahrazení libovolné rovnice soustavy součtem této rovnice s libovolnou jinou rovnicí soustavy.
3. Dosazení neznámé nebo výrazu s neznámou z jedné rovnice soustavy do libovolné jiné rovnice této soustavy.

Tyto a nejen tyto úpravy budeme nejvíce procvičovat v kapitole věnované soustavám rovnic.

<<úvod lineární rovnice>>

úvod : lineární rce : lineární nerce : kvadratické rce : kvadratické nerce : iracionální rce a nerce : rce s abs. hodnotou a parametry : rce vyšších řádů : soustavy : odkazy

Copyright (c) 2008 Jaromír Gloc. Všechna práva vyhrazena.