Zavedení lineárních rovnic
- Lineární rovnicí
-
s neznámou x, nazveme každou rovnici, kterou je možné ekvivalentními úpravami převést na tvar
ax + b = 0,
kde koeficienty a, b jsou libovolná reálná čísla.
Za podmínky, že a ≠ 0, pak pomocí dvou ekvivalentních úprav zjistíme, že kořenem takovéto rovnice je právě jedno reálné číslo 
.
Celé řešení všech lineárních rovnic spočívá v důsledné aplikaci ekvivalentních úprav rovnice a zjednodušování výrazů na obou stranách. Tím postupně zadanou rovnici upravujeme do tvaru x = k, kde k bude s největší pravděpodobností jediný kořen zadané rovnice.
Variantu s koeficientem a = 0, si rozebereme níže u vzorového příkladu, který toto předvede. Stejně tak je možné, že hodnotu k nebudeme moci použít z toho důvodu, že toto číslo nebude ležet v definičním oboru rovnice D. I to si ukážeme v některých příkladech.
Řešené příklady
-
Příklad 1
Řešte v
rovnici
-
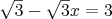
Řešení
Nezalekneme se "složitých" koeficientů a rovnou začneme řešit. Na začátku řešení příkladu určíme O a D dané rovnice. V tomto případě to bude jednoduché. O máme zadán jako
a D je určen platností výrazů na obou stranách rovnice, které ale jsou definovány pro všechny reálné hodnoty neznámé x. A tedy:
Obě strany rovnice už obsahují maximálně zjednodušené výrazy, proto se budeme snažit člen levé strany s neznámou x osamostatnit na levé straně a druhý člen převést na pravou stranu. To provedeme odečtením
od obou stran rovnice.
Výraz na pravé straně už více neupravíme, a protože na levé straně máme jen násobek x provedeme ekvivalentní úpravu vydělení obou stran rovnice číslem
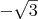. Dostaneme: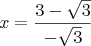
Výsledný výraz na pravé straně ještě usměrníme:
Při usměrňování zlomků vynásobíme celý
zlomek tak šikovně zapsanou jedničkou,
abychom se zbavili odmocniny ve jmenovateli.
Získali jsme tedy kořen zadané rovnice:
Sice bychom mohli výraz 
na pravé straně pomocí kalkulačky vyčíslit,
ale protože odmocnina ze tří je iracionální číslo, nemohli bychom ji zapsat
přesně a museli bychom zaokrouhlovat. Je tedy lepší jej nechat zapsaný takto.Ještě si ověříme jeho správnost provedením zkoušky. Vypočítáme hodnotu levé strany tak, že dosadíme za x hodnotu, která nám vyšla.
Hodnota pravé strany nezáleží na kořenu a platí
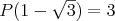, zkouška nám vyšla a můžeme provedený výpočet potvrdit zápisem
.Zbývá jen určit množinu K.
K - množina všech kořenů rce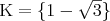 
Ukázali jsme si tedy základní postup řešení lineárních rovnic: určíme 0 a D,upravíme výrazy na obou
stranách, separujeme neznámé na jedné straně rce a pak vydělíme obě strany příslušným číslem,
aby koeficient u neznámé byl 1. Na závěr zapíšeme množinu K.
V další příkladu si ukážeme řešení lineárních rovnic v jiném oboru řešitelnosti O, než jsou reálná čísla.
Příklad 2
Řešte v
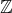rovnici
. -
Řešení
Na začátek určíme obor řešení a definiční obor:
Rovnici opět budeme řešit klasickým postupem. To, v jakém oboru řešitelnosti O celou rovnici řešíme, nemá vliv na samotný průběh řešení. Projeví se to při určování kořene.
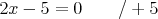
Zdánlivě nám vyšel kořen 2,5. V zadání však máme řečeno, že celou rovnici máme řešit v oboru celých čísel. Obory řešení rovnice a definiční obor jsou tedy rovny oboru celých čísel, a proto číslo 2,5, které není celé, nemůže být řešením této rovnice.
Kdybychom celou rovnici řešili v , nebo v nějaké množině, která číslo
2,5 obsahuje, samozřejmě bychom ho jako řešení uznali. Zapíšeme tedy:
Další příklad nám ukázal, že i když dokážeme dospět k rovnici ve tvaru x = k, nemusí to pro nás
znamenat, že k je kořen rovnice. Je tedy nutné na začátku řešení vždy určit definiční
obor rovnice D.
Další příklad, přestože řešený v , ukáže že ani obor řešitelnosti obsahující všechna reálná čísla nemusí být postačující, abychom uznali číslo, které nám vyjde, jako kořen.
Příklad 3
Řešte v
rovnici
.-
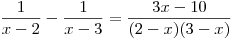Řešení
Tentokrát určení definičního oboru nebude úplně jednoduché. Obor řešení jsou všechna
a výrazy jak na levé straně, tak na pravé, obsahují zlomek, který má ve jmenovateli neznámou x. Musíme tedy určit, pro které hodnoty x by výrazy ve jmenovatelích levé i pravé strany byly nulové a neměli by pak smysl.Pro levou stranu rovnice tedy určíme podmínky:
,které upravíme na
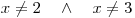.Při zjišťování podmínek platnosti výrazu na pravé straně si uvědomíme, že součin dvou výrazů je nulový, právě když je nulový alespoň jeden z nich. Proto, chceme-li zabránit tomu, aby byl jmenovatel zlomku nulový, nesmí být nulová ani jedna ze závorek. Dostaneme tedy podmínky:
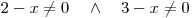,které upravíme na
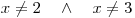, ale stejné podmínky už nám vyšly u výrazů na levé straně.Zapíšeme tedy O a D takto:
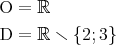
Zápis množiny v definičním oboru znamená: Všechna reálná čísla bez
2 a 3. Použité "šikmé mínus" znamená rozdíl množin.protože pro hodnoty 2 a 3 by právě tato rovnice nebyla definována (výrazy na obou stranách rovnice by neměly smysl).
Teď se teprve můžeme pustit do řešení samotné rovnice. Nejprve upravíme a co nejvíce zjednodušíme levou stranu rovnice a roznásobíme závorky ve jmenovateli pravé strany.
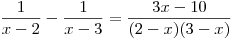
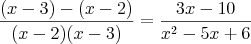
Pak výraz na pravé straně převedeme nalevo, abychom mohli oba výrazy spojit dohromady:
Převedeme na jeden zlomek:
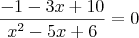
A díky určenému D, který nám zaručuje, že výraz ve jmenovateli je nenulový, můžeme celou rovnici vynásobit výrazem ve jmenovateli a dále upravovat:
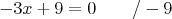
Vypadá to, že nám vyšel kořen x = 3, jenže nesmíme zapomenout na to, že nám definiční obor tuto hodnotu zakazuje. A protože
, tak K nemůže 3 obsahovat a tedy:
Opět se ukázalo, že ne vše, co nám vyjde, je automaticky kořen rce. Zároveň jsme si ukázali
užitečnost určování definičního oboru před řešením, protože jinak bychom nemohli rci
korektně upravovat.
Poslední příklad nám ukáže, že lineární rovnice nemusí mít vždy jen jeden kořen.
Příklad 4
Řešte v
rovnici
.-
Řešení
Na začátku řešení příkladu určíme O a D dané rovnice. Obor řešení je dán a protože obě strany rovnice obsahují jen výrazy definované pro všechna reálná čísla, bude i určení definičního oboru lehké.
Při samotném řešení nejprve upravíme výraz na levé straně rovnice tím, že umocníme obě závorky
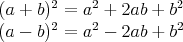a sečteme členy, které sečíst můžeme.
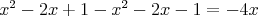
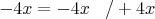
Už v tento okamžik by nám mohlo být jasné, že zřejmě nedostaneme klasické jedno řešení lineární rovnice, ale ukážeme si správný postup ještě dále
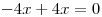
V tento okamžik ukončíme úpravu daného typu rovnice a začneme řešit, jaké kořeny má tato poslední rovnice. Ze začátku můžeme zkoušet za x dosazovat libovolná reálná čísla. Pokaždé však zjistíme, že jejich vynásobení nulou způsobí, že se celková hodnota výrazu na levé straně bude rovnat nule na straně pravé.
Nemůžeme však postupně vyzkoušet všechna reálná čísla, provedeme proto úvahu, že jakékoliv reálné číslo vynásobené nulou je nula, a tedy tato rovnice bude splněna pro všechna čísla z
. Vzhledem k určenému D bude tedy:
.
Takže si pamatujme, že upravíme-li rovnici do tvaru 0 = 0, nebo 0x = 0,
je množina K rovna vždy množině D.
Obdobně jako v posledním řešeném příkladu se můžeme setkat s rovnicemi, které upravíme na tvar
0x = k, kde k je nějaké nenulové reálné číslo. Případně se nám může stát, že rovnici upravíme do rovnosti, která neplatí (např. 5 = 3).
V takovém případě, ať bychom za x dosadili jakékoliv číslo, nikdy bychom nezískali rovnost levé a pravé strany rovnice. Proto tyto rovnice nemají žádný kořen a 
.