Soustavy rovnic
V této kapitole se budeme věnovat soustavám dvou lineárních rovnic se dvěma neznámými. Pokud příklad obsahuje více rovnic, či nerovnic, které mají platit zároveň, říkáme, že řešíme soustavu rovnic, či nerovnic. Tyto soustavy pak budou zpravidla obsahovat i více neznámých, než jen jednu ![]() Představte si soustavu: x = 3
Představte si soustavu: x = 3 ![]() x = -2. Zcela jasně neexistuje
x = -2. Zcela jasně neexistuje
takové reálné číslo, aby splňovalo obě tyto rovnice zároveň.. Na střední škole se nejčastěji budeme setkávat s příklady, kdy si počet rovnic a počet neznámých v nich odpovídá.
V této práci jsme si už ukázali soustavy dvou lineárních nerovnic s jednou neznámou a ve stejné kapitole jsme i rozebírali význam soustavy lineárních nerovnic s více neznámými.
Při řešení soustav rovnic budeme potřeboval ovládat ekvivalentní úpravy soustavy rovnic, se kterými jsme se již seznámili v úvodu této práce.

Soustavy 2 rovnic s 2 neznámými
Při řešení soustav rovnic budeme soustavu převádět ekvivalentními úpravami na základní tvar:
![]() ,
,
kde x, y jsou neznámé a koeficienty a1, a2, b1, b2, c1, c2 ![]() .
.
Z tohoto tvaru lze získat řešení různými metodami, které si představíme níže.
Soustavy dvou lineárních rovnic s dvěma neznámými mají nejčastěji právě jedno řešení (jednu uspořádanou dvojici čísel).
Některé soustavy mají nekonečně mnoho řešení. To jsou takové soustavy, ve kterých mohu alespoň jednu rovnici převést ekvivalentními úpravami na rovnici 0 = 0. ![]() Někdy se setkáte s tvrzením, že to jsou takové soustavy, kde je jedna rovnice nenulovým násobkem druhé.
Někdy se setkáte s tvrzením, že to jsou takové soustavy, kde je jedna rovnice nenulovým násobkem druhé.
Soustavy dvou rovnic také nemusí mít žádné řešení. Takové soustavy poznáme tak, že alespoň jednu rovnici ekvivalentními úpravami převedeme na tvar nepravdivé rovnosti, např.: 0 = 4. ![]() To je např. tato
To je např. tato
soustava:
![]()
Řešíme soustavu se dvěma neznámými, a tak se potřebujeme v zadání dozvědět, jakých hodnot mohou nabývat obě tyto neznámé. Nebude nám tedy již stačit zadání: "Řešte v ![]() ". Budeme se tedy potkávat se symbolem pro kartézský součin množin
". Budeme se tedy potkávat se symbolem pro kartézský součin množin ![]() , který zde nebudeme vysvětlovat, ale objasníme si, co pro nás při řešení soustav bude znamenat konkrétně.
, který zde nebudeme vysvětlovat, ale objasníme si, co pro nás při řešení soustav bude znamenat konkrétně.
Interpretujeme zápisy:
Řešte v ![]() (též zapisováno jako
(též zapisováno jako ![]() ) – znamená to, že obě neznámé mohou být reálná čísla
) – znamená to, že obě neznámé mohou být reálná čísla
Řešte v ![]() – znamená to, že abecedně první neznámá může nabývat pouze reálných kladných hodnot, zatímco abecedně druhá pouze reálných záporných hodnot.
– znamená to, že abecedně první neznámá může nabývat pouze reálných kladných hodnot, zatímco abecedně druhá pouze reálných záporných hodnot.
Řešte v ![]() – znamená to, že obě neznámé mohou nabývat jen celých hodnot bez nuly.
– znamená to, že obě neznámé mohou nabývat jen celých hodnot bez nuly.

Metody řešení soustav lineárních rovnic
Sčítací metoda
Sčítací metoda využívá porovnání součtu výrazů na levých a pravých stranách obou rovnic za účelem vyrušení jedné neznámé. Tím získáme jednu rovnici s jednou neznámou. Podrobný postup si ukážeme na následujícím příkladu.
-
Příklad 1
Řešte v
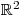 soustavu rovnic
soustavu rovnic
-
Řešení
Nejprve určíme O a D. Obor řešení máme zadán jako
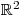 . V zadání jsou všechny výrazy platné v
. V zadání jsou všechny výrazy platné v  a tedy:
a tedy: 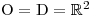 .
.Chceme-li soustavu řešit sčítací metodou, je třeba, aby koeficienty u jedné neznámé v první i ve druhé rovnici byla opačná čísla. Jinak tato metoda nemá smysl. V zadané rovnici je tato podmínka splněna u neznámé y.
Sestavíme tedy rovnici, kde na levé straně bude součet levých stran obou rovnic a na pravé straně bude součet pravých stran obou rovnic ze zadání.
 To se zapisuje takto:
To se zapisuje takto: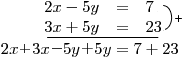
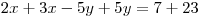
Pokud tuto rovnici totiž upravíme, vypadne nám z ní neznámá y a můžeme vypočítat x:
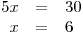
Známe-li x, dosadíme tuto hodnotu do libovolné rovnice v zadání a dopočteme y.
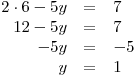
Pak už jen zapíšeme K.
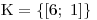
 Pozor na závorky! Tento zápis musí znamenat toto:
Pozor na závorky! Tento zápis musí znamenat toto:
"množina obsahující uspořádanou dvojici čísel 6 a 1". Početně nenáročný příklad, který nám ukázal jak sečíst dvě rovnice. Také je důležité
Početně nenáročný příklad, který nám ukázal jak sečíst dvě rovnice. Také je důležité
nezapomenout vypočítat obě neznámé, ne jen jednu.

Dosazovací metoda
Dosazovací metodu si opět nejlépe představíme na příkladu.
-
Příklad 2
Řešte v
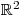 soustavu rovnic
soustavu rovnic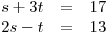
-
Řešení
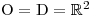
Při dosazovací metodě je vhodné mít u jedné neznámé v rovnici koeficient 1. Tu si pak vybereme a ekvivalentními úpravami upravíme rovnici tak, abychom vybranou neznámou osamostatnili na jedné straně rovnice. V zadání tomu vyhovuje neznámá s v první rovnici.
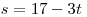
 Tento zápis nazýváme vyjádření s z první rce.
Tento zápis nazýváme vyjádření s z první rce.Nyní výraz, který máme na pravé straně této rovnice dosadíme do druhé rovnice
 Nikdy nesmíme dosadit zpět do té rovnice, ze které jsme tu neznámou vyjadřovali. místo neznámé s. Získáme tím zase jednu rovnici s jednou neznámou, kterou vyřešíme.
Nikdy nesmíme dosadit zpět do té rovnice, ze které jsme tu neznámou vyjadřovali. místo neznámé s. Získáme tím zase jednu rovnici s jednou neznámou, kterou vyřešíme.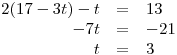
Další postup už je stejný jako u sčítací metody, jen tentokrát nemusíme vypočtenou hodnotu t dosazovat do rovnice v zadání, ale můžeme ji dosadit do rovnice
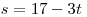 , ze které jednodušeji vypočteme s.
, ze které jednodušeji vypočteme s.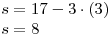
Opět zapíšeme K.
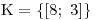
 Samozřejmě nemusíme vyjadřovat z rovnic jen neznámou, která má u sebe koeficient 1,
Samozřejmě nemusíme vyjadřovat z rovnic jen neznámou, která má u sebe koeficient 1,
jen pak budeme počítat s "horšímy" výrazy.
Obě tyto metody jsou univerzální, ale některé soustavy se lépe řeší sčítací, jiné dosazovací metodou. Kdy je výhodné tyto metody použít je zmíněno na začátku obou vzorových příkladů. ![]() Existují příklady, kdy ani dosazovací ani sčítací metoda nejsou úplně ideální a aby je šlo aplikovat, je potřeba zadání
Existují příklady, kdy ani dosazovací ani sčítací metoda nejsou úplně ideální a aby je šlo aplikovat, je potřeba zadání
nejprve upravit. Někdy i za cenu toho, že pak následně počítáme se zlomky, velkými čísly, nebo dokonce odmocninami.
Existují i další metody řešení soustav, ale s těmi se seznámíme až v dalších kapitolách, protože se uplatňují především u soustav více rovnic s více neznámými.

Řešené příklady
-
Příklad 3
Řešte v
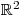 soustavu rovnic:
soustavu rovnic: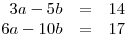
-
Řešení
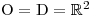
Mohli bychom řešit soustavu pomocí jakékoliv výše uvedené metody, ale zkusíme něco jiného. Vynásobíme obě strany první rovnice dvěma:
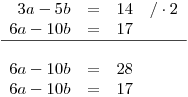
Dostali jsem nyní soustavu dvou rovnic, které mají stejné levé strany, ale na pravé straně jsou jiná čísla. Je zřejmé, že tato soustava nebude mít žádné řešení, protože neexistují taková čísla, která by tyto podmínky splnila.
Proto:
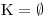 .
. Pokud bychom obě rce řešili třeba sčítací metodou, dospěli bychom k podobnému závěru.
Pokud bychom obě rce řešili třeba sčítací metodou, dospěli bychom k podobnému závěru.
Po sečtení obou rovnic bychom totiž dostali rovnici 0 = 11 a podle ní bychom usoudili,
že soustava nebude mít žádné řešení.
-
Příklad 4
Řešte v
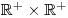 soustavu rovnic:
soustavu rovnic: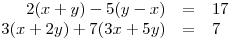
-
Řešení
O = D =
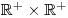
Nejprve si celou soustavu upravíme do základního tvaru:
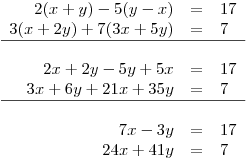
Dostali jsme soustavu, kde není úplně zřejmé, kterou z výše uvedených metod použít. Je tedy jedno jakou zvolíme, proto vybereme třeba dosazovací.
Z první rovnice vyjádříme neznámou y:
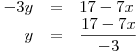
Vyjádření y dosadíme do druhé rovnice a vypočteme x:
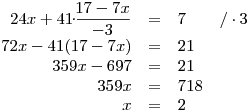
Ještě dopočítáme y, a to dosazením do vyjádření y z první rovnice:
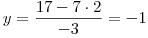
Hodnota y nám vyšla záporná, ale my celou soustavu řešíme v
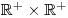 . Proto toto řešení nemůžeme uznat, a tedy tato soustava v daném O nemá žádné řešení.
. Proto toto řešení nemůžeme uznat, a tedy tato soustava v daném O nemá žádné řešení.Proto
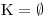
 Stačí, aby jeden z kořenů neležel v D, a již to znamená,
Stačí, aby jeden z kořenů neležel v D, a již to znamená,
že celou n-tici vypočtených kořenů nemůžeme uznat za řešení soustavy.
