Soustava lineárních nerovnic s jednou neznámou
Oproti jednoduchým nerovnicím jsou soustavy lineárních nerovnic s jednou neznámou příklady, kdy na hodnotu neznámé neklademe jen jednu podmínku (nerovnici), ale více. Nerovnic v soustavě může být více než dvě, ale nejčastěji se setkáme právě se soustavami dvou nerovnic s jednou neznámou.
Kromě soustav nerovnic s jednou neznámou můžeme mít i soustavu nerovnic s více neznámými. Takové úlohy ale už nespadají do středoškolské matematiky, proto o nich najdete jen zmínku na konci této kapitoly.
Postup pro řešení soustavy nerovnic bude následující:
- Určíme O a D společné pro celou soustavu (pro všechny nerovnice).
- Určíme množiny kořenů K1, K2… pro každou nerovnici zvlášť.
- Uděláme průnik všech množin K1, K2…, které nám vyšly. Tím získáme K celé soustavy, neboli všechna x, která jsou řešením všech nerovnic současně.
Řešené příklady
-
Příklad 1
Řešte v
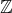soustavu nerovnic
. -
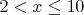Řešení
Ačkoliv to tak nevypadá, tak se v tomto příkladu jedná o soustavu dvou nerovnic s jednou neznámou x. Daný příklad bychom totiž mohli rozepsat na dvě nerovnice:
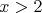a 
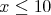,které mají platit současně.
Začneme standardně, určíme O a D, které platí pro obě nerovnice zároveň.
Pak každou nerovnici vyřešíme zvlášť. Začneme první:
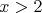
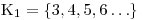
a pokračujeme druhou:
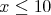
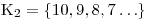
Na závěr určíme K jako průnik K1 ∩ K2
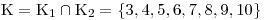
Jak tento příklad ukázal, opravdu řešení soustav nerovnic s jednou neznámou není nic těžkého.
Dokonce nám dané nerovnice kořeny tak omezily, že jsme je byli schopni vypsat
ve výsledném K všechny.
-
Příklad 2
Řešte v
soustavu nerovnic
. -
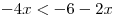
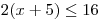Řešení
Každou nerovnici opět vyřešíme zvlášť:
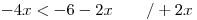
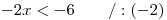
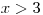
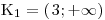
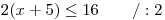
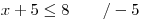
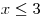
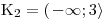
Při řešení nerovnic stále nesmíme zapomínat, že při dělení obou stran nerovnice záporným číslem se nám otočí znaménko nerovnosti.
Výsledná množina K bude opět průnik K1 ∩ K2.
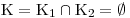
Výjimečnost tohoto příkladu je v tom, že předvedl soustavu nerovnic o jedné neznámé, která nemá
žádné řešení. Sice to "nevyšlo jen těsně", ale přece.
Soustava nerovnic pro více neznámých
Nejčastěji se setkáváme s dvěma nerovnicemi s dvěma neznámými, a to konkrétně x a y. Tyto dvě neznámé totiž pak interpretujeme jako souřadnice nějakého bodu v rovině a zadané dvě nerovnice jako podmínky pro jeho souřadnice. Tedy hledáme body roviny, které svými souřadnicemi vyhovují daným nerovnicím.
Pokud máme tři nerovnice pro tři neznámé, hledáme
body z trojrozměrného prostoru, jejichž souřadnice splňující dané nerovnosti.
Toto už ale nepatří do běžného učiva na středních školách. Navíc by bližší vysvětlování postupu řešení znamenalo vysvětlit grafy lineární funkcí, a základy planimetrie. Vše je ale velmi dobře zpracováno v Polák [8].