Úlohy k opakování
-
Úloha 1
Řešte v
 soustavu nerovnic pro neznámou x
soustavu nerovnic pro neznámou x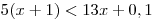
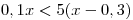 .
. -
 Určíme O a D.
Určíme O a D.

 Nevyřešíme tu první nerci?
Nevyřešíme tu první nerci?
 Začneme s tou druhou nercí?
Začneme s tou druhou nercí?
Roznásobíme závorku na levé straně nerce a separujeme neznámou na straně pravé.
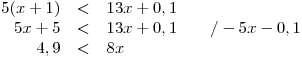
 Vydělíme nerci koeficientem u x, tedy 8
Vydělíme nerci koeficientem u x, tedy 8
Vydělíme nerci 8.
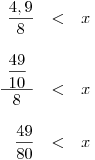
 ZapíšemeK1.
ZapíšemeK1.
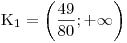
Roznásobíme závorku na pravé straně a separujeme neznámou vlevo.
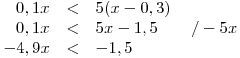
 Vydělíme nerci koeficientem u x, tedy −4,9.
Vydělíme nerci koeficientem u x, tedy −4,9.
Vydělíme nerci −4,9 a otočíme znaménko nerovnosti!
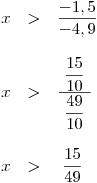
 ZapíšemeK2.
ZapíšemeK2.
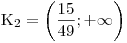
 Určíme výsledné K průnikem K1 a K2. Ale které číslo je větší:
Určíme výsledné K průnikem K1 a K2. Ale které číslo je větší: 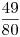 nebo
nebo 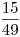 ?
?
K určení průniku K1 a K2, potřebujeme zjistit, které z čísel
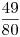 a
a 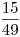 je větší.
je větší.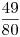 ?
? 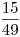
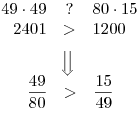
 Určíme výsledné K.
Určíme výsledné K.
Zjistíme průnik K1 a K2:
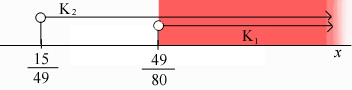
a tedy:
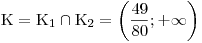
 Jednoduchá soustava dvou nerovnic s jednou neznámou se komplikuje pouze použitím
Jednoduchá soustava dvou nerovnic s jednou neznámou se komplikuje pouze použitím
desetinných čísel, díky kterým se pak složitěji určuje průnik K1 a K2. Je proto potřeba dávat
obzvlášť pozor na numerické chyby.

-
Úloha 2
Řešte v
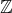 soustavu nerovnic pro neznámou t
soustavu nerovnic pro neznámou t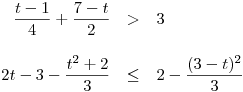 .
. -
 Určíme O a D.
Určíme O a D.
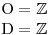
 Nezačneme něco dělat s tou první nercí?
Nezačneme něco dělat s tou první nercí?
 Pustíme se do té druhé nerce?
Pustíme se do té druhé nerce?
Vynásobením celé nerce číslem 4 se zbavíme zápisu pomocí zlomků.
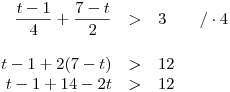
 Separujeme t.
Separujeme t.
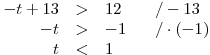
 ZapíšemeK1.
ZapíšemeK1.
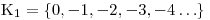
Vynásobením celé nerce číslem 3 se zbavíme zápisu pomocí zlomků.
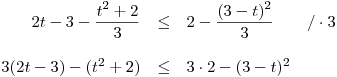
 Roznásobíme závorky na lévé straně a umocníme
Roznásobíme závorky na lévé straně a umocníme
závorku napravo. Pak sečteme spolu, co půjde…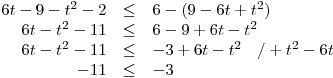
 Úpravami jsme dostali nerovnost, která platí pro
Úpravami jsme dostali nerovnost, která platí pro
jakoukoliv hodnotu t, proto jednoduše určíme K2.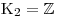
 Určíme výsledné K průnikem K1 a K2. To by neměl být problém…
Určíme výsledné K průnikem K1 a K2. To by neměl být problém…
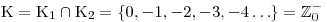
 Což se dá také zapsat jako
Což se dá také zapsat jako 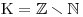 .
. Stále nesmíme zapomínat, že pokud výrazy na obou stranách nerce násobíme záporným
Stále nesmíme zapomínat, že pokud výrazy na obou stranách nerce násobíme záporným
číslem, otočíme znaménko nerovnosti. Zároveň jsme si ukázali, že existují nerce, které mají
množinu kořenů rovnu jejich definičnímu oboru, jako byla druhá nerce v této soustavě.

-
Úloha 3
Řešte v
 nerovnici pro neznámou x
nerovnici pro neznámou x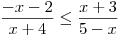 .
. -
 Určíme O a D.
Určíme O a D.
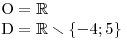
 Převedeme vše z pravé strany na levou, abychom tam získali nulu.
Převedeme vše z pravé strany na levou, abychom tam získali nulu.
Na pravé straně nerce se snažíme získat nulu.
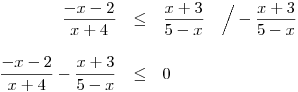
 Zlomky na levé straně nerce odečteme
Zlomky na levé straně nerce odečteme
(převedeme na společný jmenovatel a upravíme čitatel).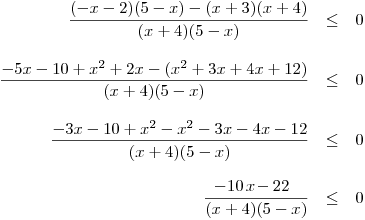
 Určíme nulové body lineárních dvojčlenů.
Určíme nulové body lineárních dvojčlenů.
Nulové body lineárních dvojčlenů:
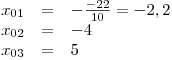
 Sestavíme tabulku.
Sestavíme tabulku.
(− 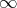 ; −4)
; −4)−4 (−4 ; −2,2) −2,2 (−2,2 ; 5) 5 (5 ; 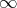 )
)−10x − 22 + + + 0 − − −  Vyplníme první
Vyplníme první
řádek tabulky.x + 4 − 0 + + + + +  Vyplníme druhý
Vyplníme druhý
řádek tabulky.5 − x + + + + + 0 −  Vyplníme třetí
Vyplníme třetí
řádek tabulky.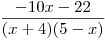
− N + 0 − N +  Ze znamének v tabulce určíme výsledná znaménka celého zlomku v daných sloupcích.
Ze znamének v tabulce určíme výsledná znaménka celého zlomku v daných sloupcích.
 Určíme, které sloupečky vyhovují nerovnici.
Určíme, které sloupečky vyhovují nerovnici.
 Určíme K.
Určíme K.
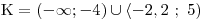
 Příklad nerce v podílovém tvaru, ve kterém začínáme se zlomky s neznámými na obou
Příklad nerce v podílovém tvaru, ve kterém začínáme se zlomky s neznámými na obou
stranách rovnice. Jak je ale vidět, neřeší se tento příklad jinak, než ten, který jsme si představili
ve výkladu nerovnic v podílovém tvaru. Jen vyžaduje trochu více "počítání".

Testíky
Klikněte na otazník u odpovědi, o které myslíte, že je dobře, a smajlík vám prozradí, zda jste odpověděli správně. U každého příkladu je jen jedna správná možnost.
|
Řešte v
|
Řešte v
|
|
Řešte v
|
Řešte v
|
Řešení dalších úloh si můžete vyzkoušet v testu za lineárními rovnicemi a nerovnicemi.

