Pojem lineární dvojčlen
- Lineárním dvojčlenem
- nazveme výraz ve tvaru ax + b, kde x je neznámá, a, b jsou reálná čísla a a ≠ 0.
Naší snahou v této kapitole bude naučit se řešit nerovnice v podílovém tvaru, tedy nerovnice jejichž jedna strana se dá zapsat jako podíl libovolného počtu součinů lineárních dvojčlenů v čitateli i jmenovateli. Druhá strana nerovnice je nulová. Jedná se o nerovnice, které mohou vypadat například takto:
,
ale třeba i takto:
,
Tato nerovnice sice v čitateli nemá ani jeden lineární dvojčlen,
ale princip řešení bude obdobný jako u těch, které ho mají.
nebo takto:
.
Takovéto nerovnice se nazývají nerovnice v součinovém tvaru. Řeší se ale obdobně, proto je nebudeme vyčleňovat.
Jak řešit lineární nerovnice v podílovém tvaru
-
Příklad 1
Řešte v
nerovnici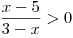 
. -
Řešení
Nejprve určíme O a D. Levá strana obsahuje zlomek s neznámou ve jmenovateli, proto musíme určit, jaké hodnoty nesmí x nabývat, aby byl definován. Hned je ale vidět, že x ≠ 3.
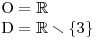
Na tuto nerovnici budeme nahlížet jako na zlomek, který má být kladný. To bude splněno, když jmenovatel i čitatel budou kladní nebo oba budou záporní. Toto můžeme zapsat jako:
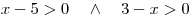
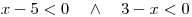
Dále můžeme řešit dvě soustavy dvou lineárních nerovnic a sjednotit jejich řešení.
Tato varianta by asi v tomto konkrétním případě byla jednodušší, ale obecně to pro tento
typ příkladů neplatí. Navíc si chceme ukázat řešení pomocí tabulky s nulovými body, a tak
variantu soustav lineárních nerovnic protentokrát zavrhneme. Nebo budeme uvažovat dále.Hledáme-li, pro které hodnoty x je čitatel kladný, můžeme si naznačit následující schéma:
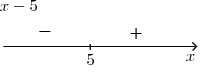
Na číselné ose je vyznačeno číslo 5, pro které bude lineární dvojčlen x − 5 roven nule. Nazveme ho nulový bod. Jednoduchým dosazením několika hodnot vidíme, že pro všechna x menší než nulový bod, bude dvojčlen nabývat záporných hodnot, a pro všechna x větší než nulový bod hodnot kladných.
Obdobný obrázek si uděláme i pro dvojčlen ve jmenovateli:
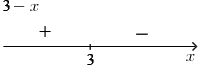
Tentokrát jsou znaménka u částí číselné osy naopak. To je dáno mínusem před x ve dvojčlenu.
Tím jsme určili, pro které hodnoty x bude čitatel i jmenovatel kladný, nebo záporný. Ale jak to dáme dohromady?
Vytvoříme tabulku, jejíž první řádek bude obsahovat části celé číselné osy. Ty získáme rozdělením celé číselné osy podle nulových bodů. Získáme tak otevřené intervaly mezi nulovými body, dva otevřené intervaly vně nejmenšího a největšího z nulových bodů a dále jednoprvkové množiny obsahující získané nulové body.
V tomto konkrétním příkladě to tedy budou dvě jednoprvkové množiny {3} a {5}, jeden otevřený interval mezi těmito body (3 ; 5) a dva vnější otevřené intervaly (−
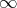; 3) a (5 ; 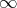).V dalších řádcích určíme do jednotlivých buněk tabulky znaménka příslušných lineárních dvojčlenů na úsecích číselné osy, které odpovídají zapsanému intervalu, nebo množině, v prvním řádku.
Pokud nevíme jaké znaménko do příslušné buňky tabulky napsat, stačí si z nahoře uvedeného
intervalu zvolit libovolné číslo a to dosadit do dvojčlenu, který je napsán na počátku řádku.
Vyjde nám číslo, jehož znaménko je stejné jako znaménko dvojčlenu v příslušném intervalu.(− 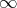; 3)3 (3 ; 5) 5 (5 ; 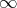)x – 5 − − − 0+ 3 – x + 0 Ve sloupečku s nulovým bodem daného dvojčlenu bude
samozřejmě dvojčlen nulový.− − −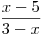 
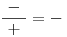
NELZE Kdybychom na začátku řešení příkladu zapomněli určit
podmínky platnosti, resp. D, tak by nás tady mělo trknout
dělení nulou a měli bychom to napravit!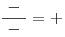
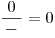
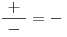
Všimněte si, že nemusíme speciálně počítat znaménka ve všech buňkách tabulky. U lineárních
dvojčlenů platí, že jejich znaménko v celém intervalu od −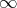 až k nulovému bodu je přesně opačné
než v celém intervalu od nulového bodu do +.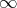
Takže stačí napsat nulu do sloupečku s nulovým bodem a vypočítat znaménko výrazu v libovolném
jiném sloupečku. To pak můžeme napsat i do všech ostatních buněk tabulky na stejné straně
od nulového bodu. Na opačnou stranu pak napíšeme znaménka opačná.V posledním řádku tabulky vyhodnotíme výsledné znaménko celého zlomku. Jednoduše si představíme, že dělíme-li kladné číslo záporným dostaneme vždy záporné, dále že nulou dělit nemůžeme, že nula dělená něčím záporným je nula apod.
Při pohledu na zadání celého příkladu zjistíme, že hledáme případ, kdy je celý zlomek větší než nula, tedy kladného znaménka. Najdeme všechny sloupečky, ve kterých nám v posledním řádku tabulky vyšlo kladné znaménko, a do množiny kořenů K sjednotíme všechny množiny z těchto sloupečků.
V tomto případě je pouze v prostředním sloupečku kladné znaménko, a tedy pouze interval (3 ; 5) je řešením celé nerovnice.
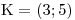
Ne vše, co jsme psali u tohoto příkladu, je nutné provádět u řešení každého příkladu. Některé věci
zde uvedené sloužily především k vysvětlení principů, na kterých funguje závěrečná tabulka.
Proto u příštích příkladů je dělat nebudeme a ušetříme čas i místo.
Řešené příklady
-
Příklad 2
Řešte v
nerovnici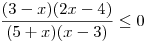 
. -
Oproti předchozím příkladům nebudeme nejdříve určovat O a D, ale určíme nulové body všech čtyř lineárních dvojčlenů v rovnici.
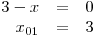
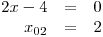
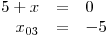
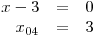
Teď teprve přijde čas na obor řešení rovnice a definiční obor. Už při letmém pohledu na zadání rovnice bychom si měli všimnout neznámé ve jmenovateli zlomku. Měli bychom si hned uvědomit, že budeme určovat podmínky platnosti tohoto výrazu na levé straně nerovnice.
Vzhledem k tomu, že jmenovatel je ve tvaru součinu dvou výrazů, můžeme provést úvahu, že součin je nulový, právě když je alespoň jeden z činitelů nulový. A už přece víme, kdy to nastane, protože jsme si určili nulové body výrazů ve jmenovateli. Takže stačí zakázat, aby x nabývalo hodnot −5 a 3.
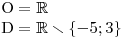
Nyní můžeme sestavit tabulku. Dva nulové body jsou stejné, proto se bude číselná osa dělit jen na 7 částí (3 nulové body, 2 intervaly mezi nimi a 2 intervaly vně).
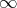(− ;−5)−5 (−5;2) 2 (2;3) 3 (3; 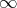)3 − x + + + + + 0 − 2x − 4 − − − 0 + + + 5 + x − 0 + + + + + x − 3 − − − − − 0 +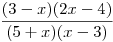 
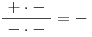
N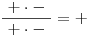 
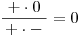
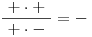
N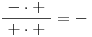 
Hledáme případ, kdy je zlomek menší nebo roven nule. Označíme si tedy všechny sloupečky, ve kterých nám v posledním řádku vyšlo mínus, nebo nula. Množiny, které tyto sloupce reprezentují, pak sjednotíme a dostaneme K.
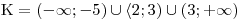
Všimněte si, že jsme dva sousední sloupečky sloučili do jednoho
intervalu. Vlastně jsme provedli: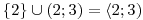
. Na tomto příkladě bylo už jasně vidět, že metoda řešení pomocí tabulky je daleko efektivnější,
než třeba převedení na soustavu lineárních nerovnic. V tomto případě bychom museli řešit
osm různých soustav čtyř nerovnic, abychom vyčerpali všechny možnosti, kdy zlomek na levé
straně nerovnice může být menší nebo roven nule.
Doposud jsem řešili pouze nerovnice, které na jedné straně měly nulu. Může se ale stát, že zadaná nerovnice bude mít obě strany nenulové. Co s tím budeme dělat, si ukážeme v dalším příkladě.
-
Příklad 3
Řešte v
nerovnici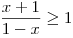 
. -
Řešení
Ačkoliv se na první pohled zdá, že je tato nerovnice podobná těm předchozím, není to tak úplně pravda. Tuto nerovnici je nutné nejprve upravit do tvaru, kdy je na jedné straně nerovnice nula. Pokud toto neprovedeme a rovnou začneme určovat nulové body a sepisovat tabulku, rozhodně nedosáhneme řešení.
Ještě před tím, než začneme danou rovnici upravovat, si určíme O a D.
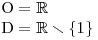
A teď se můžeme pustit do úprav. Obecně je jedno, na které straně nerovnice získáme nulu, ale v tomto případě bude jednodušší přenést číslo 1 z pravé strany pomocí ekvivalentních úprav nalevo a "vynulovat" tak pravou stranu.
Nyní levou stranu upravíme na jeden zlomek. Převedeme tedy oba zlomky na společný jmenovatel a pak je od sebe odečteme.
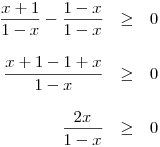
Tím jsme celou nerovnici upravili do známého tvaru a už můžeme postupovat standardně: nulové body, tabulka…
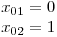
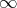(− ;0)0 (0;1) 1 (1; 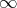)2x − 0 + + + 1 − x + + + 0 −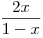 
− 0 + N − Na závěr určíme K:
Sice jsme si zde ukázali jen jednoduchý příklad, kdy nerovnice měla na pravé straně místo nuly
čislo 1, ale lze snadno nahlédnout, že postup řešení by byl stejný, i kdyby byly na obou stranách
nerovnice zlomky s neznámými, či jiné výrazy.
V této kapitole jsme se záměrně nevěnovali tzv. nerovnicím v součinovém tvaru, a to z toho důvodu, že jejich řešení je obdobné jako řešení nerovnic v podílovém tvaru. Opět se určují nulové body jednotlivých lineárních dvojčlenů, sestavuje se tabulka a na závěr se vyhodnocuje znaménko celého součinu.