Úlohy k opakování
-
Úloha 1
Řešte v
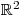soustavu rovnic:
-
Určíme O, D a obě rovnice v soustavě převedeme na základní tvar.
O = D =
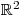
Převedeme ekvivalentními úpravami obě rovnice na základní tvar.
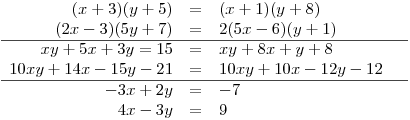
Vypočteme x sčítací metodou.
Před použitím sčítací metody si obě rovnice v soustavě ještě trochu upravíme.
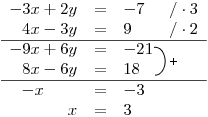
Dopočteme y dosazením.
Dosadíme vypočtenou hodnotu x do první rovnice těsně před sečtením rovnic.
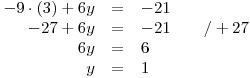
Zapíšeme K.
Z vypočtených hodnot x a y vytvoříme uspořádanou dvojici a zapíšeme K.
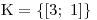
Tuto jednoduchou soustavu dvou rovnic s dvěma neznámými komplikoval snad jen úvod,
kdy jsme museli soustavu upravit na základní tvar.
-
Úloha 2
Řešte v
soustavu rovnic
-
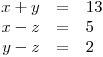
Určíme O, D a začneme soustavu řešit Gaussovou eliminační metodou.
O = D =
Při řešení této soustavy Gaussovou eliminační metodou necháme první rovnici tak jak je zadána. Její koeficient u x je 1 a to se nám hodí.
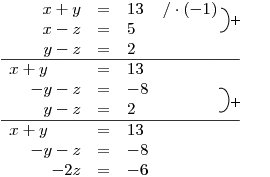
Vypočteme x, y, z.
Vypočteme nejprve hodnotu z, pak y, a na závěr x.
z = 3 
Zapíšeme K.
Řešení pomocí Gaussovy eliminační metody je často velmi rychlé a efektivní. Pokud máme
v soustavě zadány rovnice, které neobsahují některé neznámé, můžeme je v algoritmu
této metody efektivně využít. V této úloze jsme toto využili u třetí rce,
kterou jsme v první kroku metody nechali bez úprav.
-
Úloha 3
Řešte v
soustavu rovnic:
-
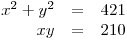
Určíme O a D a začneme soustavu řešit dosazovací metodou.
O = D =
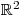
Kdybychom chtěli z druhé rovnice vyjádřit třeba x, museli bychom celou rci vydělit y. Hodnota proměnné y by ale mohla být nulová a dělit rovnici nulou je zakázaná úprava. Rozdělíme tedy řešení soustavy do dvou větví.
Co když y = 0?
Pro y = 0 nemůžeme druhou rovnici vydělit y, ale všimneme si, že soustava nemá žádné řešení. Po dosazení této hodnoty za y do druhé rce, získáme rci 0x = 210, která nám tvrzení o neřešitelnosti této soustavy potvrzuje.
Co když y ≠ 0?
Je-li y ≠ 0, pak z druhé rovnice můžeme vyjádřit x a dosadit ho do první rovnice
Vyřešníme bikvadratickou rci substitucí [y2 = t].
Získali jsme bikvadratickou rci, která se nejlépe řeší substitucí [y2 = t]
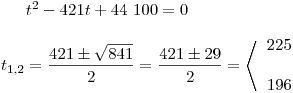
Vypočtené hodnoty t dosadíme zpět do předpisu substituce a vypočítáme příslušná y.
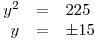
Pro vypočtené hodnoty y dopočteme příslušná x.
Pro vypočtené hodnoty y dopočteme příslušná x dosazením do druhé zadané rce.
pro y = 15
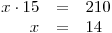
pro y = −15
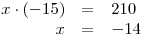
pro y = 14
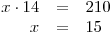
pro y = −14
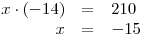
Zapíšeme K.
V množině všech řešení dané soustavy K nakonec budou čtyři uspořádané dvojice.
Tato soustava v sobě ukrývala bikvadratickou rovnici. V soustavách dvou rovnic,
z nichž je alespoň jedna kvadratická, je tato "zákeřnost" poměrně běžná
a je tedy vhodné umět tyto speciální rovnice 4. stupně řešit.
Testíky
Klikněte na otazník u odpovědi, o které myslíte, že je dobře, a smajlík vám prozradí, zda jste odpověděli správně. U každého příkladu je jen jedna správná možnost.
|
Určete kolik má daná soustava řešení v
|
Určete kolik má daná soustava řešení v
|
|
Určete kolik má daná soustava řešení v
|
Určete kolik má daná soustava řešení v
|
soustava nemá žádné řešení
Řešení dalších úloh si můžete vyzkoušet v testu v následující kapitole.