Vietovy vzorce
Mezi kořeny x1, x2 a koeficienty a, b, c kvadratické rovnice ax2 + bx + c = 0 platí tyto vztahy:
![]()
![]()
Zdůvodnění tohoto poznatku je velmi jednoduché, stačí si za x1 a x2 dosadit ![]() a
a ![]() , tyto výrazy sečíst (či vynásobit) a upravit.
, tyto výrazy sečíst (či vynásobit) a upravit.
Tyto vzorce se nazývají Vietovy podle francouzského matematika, který se zabýval kvadratickými rovnicemi.

Aplikace Vietových vzorců
Mějme kvadratickou rovnici ax2 + bx + c = 0, která má dva reálné kořeny x1 a x2.
Pak kvadratický trojčlen ax2 + bx + c se dá rozložit na součin lineárních dvojčlenů takto:ax2 + bx + c = a(x − x1)(x − x2).
![]() Neboli mohu kvadratickou rci převést na tvar: a(x − x1)(x − x2) = 0.
Neboli mohu kvadratickou rci převést na tvar: a(x − x1)(x − x2) = 0.
Chceme-li si předchozí tvrzení ověřit, opět to nebude náročné. Pokud vyjdeme z výrazu
a(x − x1)(x − x2), roznásobíme jej a dosadíme za ![]() a za
a za ![]() , dostaneme ax2 + bx + c.
, dostaneme ax2 + bx + c.
Má-li kvadratická rovnice jen jeden kořen x1, pak jej bereme jako tzv. dvojnásobný kořen a výše uvedené tvrzení pro ni platí také s tím, že v rozkladu kvadratického trojčlenu zax2 dosadíme x1. Nemá-li kvadratická rovnice žádné reálné kořeny, pak se trojčlen rozložit nedá.
Této vlastnosti se nejvíce využívá při práci s výrazy, kde se objevují kvadratické trojčleny, a při sestavení kvadratické rovnice, známe-li její kořeny.

Ukázky použití
-
Příklad 1
Upravte daný výraz a určete, kdy má smysl:

-
Řešení
Podle výše uvedeného návodu rozložíme kvadratické trojčleny v čitateli i jmenovateli na součiny lineárních dvojčlenů. K tomu potřebujeme získat kořeny příslušných kvadratických rovnic.
Vypočteme kořeny rovnice
 :
:
Vypočteme kořeny rovnice
 :
: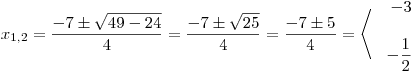
Tedy můžeme kvadratické trojčleny ve zlomku přepsat jako

a tyto výrazy pak dosadit do zlomku, kde pak můžeme krátit.
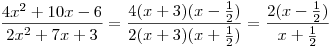
Na závěr určíme podmínky platnosti výrazu v zadání příkladu. Celý zlomek je definován jen pro ta x, pro která není jmenovatel zlomku nulový. Neboli není definován pro kořeny rce
 . Ty už jsme ale vypočetli, a tak jednoduše můžeme napsat podmínky platnosti
. Ty už jsme ale vypočetli, a tak jednoduše můžeme napsat podmínky platnosti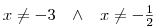 .
. Toto je typický příklad použití Vietových vzorců, resp. rozložení kvadratického trojčlenu na součin
Toto je typický příklad použití Vietových vzorců, resp. rozložení kvadratického trojčlenu na součin
lineárních dvojčlenů. Nezapomeňte ale, že ne každý kvadratický trojčlen se dá takto rozložit!
