Co to jsou iracionální nerovnice
Iracionálními nerovnicemi se nazývají nerovnice, ve kterých se vyskytuje neznámá pod odmocninou.
Při řešení iracionálních nerovnic je velmi důležité dbát na ekvivalentnost úprav, které s nerovnicí provádíme. U nerovnic totiž nemáme možnost provádět zkoušku dosazením. Nemůžeme tedy ověřovat, zda všechna vypočítaná čísla jsou kořeny i původní nerovnice. 
Až na výjimky, kdy K vyjde jako
množina obsahující několik celých čísel.
Vzhledem k tomu,že se nedá sestavit univerzální postup pro řešení iracionálních nerovnic, ukážeme si jen řešení několika typických příkladů, se kterými se ve středoškolské výuce můžeme setkat.
Řešené příklady
-
Příklad 1
Řešte v
nerovnici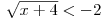 
. -
Řešení
Nejprve si uvědomíme, že výraz x + 4 pod odmocninou musí být nezáporný, neboli:
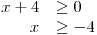
Díky této podmínce se nám teď lépe určí definiční obor nerovnice.
Při samotném řešení nerovnice
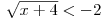jako první vyhodnotíme znaménka obou stran.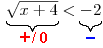
Na levé straně nerovnice je vše schováno pod druhou odmocninou, tedy pro jakoukoliv hodnotu x z D bude levá strana nezáporná. Pravá strana je vždy záporná, a proto nemůžeme použít ekvivalentní úpravu umocnění obou stran rovnice.
Musíme tedy najít nějaký jiný postup, který nás přivede k řešení nerovnice. Jak jsme již určili, obě strany nerovnice mají znaménka nezávislá na x, a tak zkusíme prozkoumat zadanou nerovnost. Ta vyžaduje, aby něco, co je vždy nezáporné (tedy kladné, nebo nulové), bylo menší než −2. To je ale nemožné! Tato nerovnost proto nebude pro žádnou hodnotu x splněna a tudíž nerovnice nemá žádný kořen.
Po této úvaze už jen stačí zapsat K.
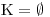
Pokud obě strany nerce mají nestejné znaménko, které nezávisí na hodnotě x, nemůžeme obě
strany umocnit a řešení úvahou s porovnáním znamének stran rovnice je skoro jediné možné.
Následující příklad ukáže možnost obdobnou, jen s opačným znaménkem nerovnosti.
-
Příklad 2
Řešte v
nerovnici 
. -
Řešení
Opět nejprve pomocí podmínek platnosti výrazu na levé straně nerovnice určíme definiční obor D.
A tedy:
Opět nemůžeme obě strany umocnit, protože nezávisle na hodnotě x mají opačná znaménka.
Aplikujeme-li ale stejnou úvahu jako minule, můžeme zadanou nerovnost interpretovat jako požadavek, aby něco nezáporného bylo větší nebo rovno −4. To je ale splněno vždy, tedy pro každou dovolenou hodnotu x, a tak kořenem nerovnice budou všechna x z D.
Opět jsme si ukázali iracionální nerci s nestejnými znaménky levé a pravé strany, nezávislými
na hodnotě x. Nemůžeme použít úpravu umocnění obou stran nerce, ale místo toho vše vyřešíme
úvahou a porovnáním znamének stran nerovnice.
Další příklad ukáže složitější řešení iracionálních nerovnic.
-
Příklad 3
Řešte v
nerovnici 
. -
Řešení
Jako vždy, i tentokrát začneme určováním, pro které hodnoty x je definován výraz na levé straně nerovnice, abychom určili definiční obor celé nerovnice.
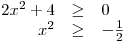
Tato nerovnost je ale splněna pro všechna reálná čísla, která bychom dosadili za x, a tedy:
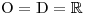
Samotné řešení nerovnice začneme určováním znamének výrazů na obou stranách nerovnice.
Odmocnina na levé straně bude pro všechny možné hodnoty x kladná, ale znaménko výrazu na pravé straně nerovnice se bude s měnící se hodnotou x měnit takto: Pro x ≥ 0 bude výraz 4x nezáporný, pro x < 0 bude záporný.
Abychom mohli dále postupovat ekvivalentními úpravami, budeme muset řešení nerovnice rozdělit na dva případy: pro x nezáporná a pro x záporná.
pro x ≥ 0 pro x < 0 Vlastně budeme dál řešit rovnici v zadání, jen omezíme její definiční obor na 
.Abychom se nepřipravili o žádné řešení zadané nerovnice, podíváme se i na její řešení v definičním oboru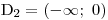 
Nyní jsou obě strany nerovnice nezáporné, a tak můžeme obě umocnit na druhou a upravit.
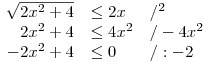
A po poslední ekvivalentní úpravě získáme kvadratickou nerovnici:
Vypočteme si kořeny příslušné kvadratické rovnice. Ať už pomocí vzorečku s diskriminantem, nebo rozkladem pomocí vzorce
, získáme:
Načrtneme si graf příslušné kvadratické funkce a určíme z něj řešení kvadratické nerovnice
.
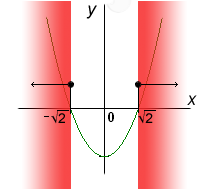
Vidíme, že nerovnici by vyhovovala
, jenže v této větvi řešení máme dovolena jen x nezáporná.Proto
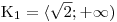.Dostali jsme nerovnici s opačnými znaménky jednotlivých stran a nemůžeme ji ekvivalentně upravit umocněním obou stran nerovnice.
Je ale vidět, že znaménka obou stran budou stejná, pro všechna x < 0. Vidíme, že kladný výraz na pravé straně má být menší nebo roven zápornému výrazu na straně pravé. To samozřejmě nebude nikdy splněno a proto tato nerovnice nebude mít pro x < 0 žádný kořen.
Na závěr jen provedeme sjednocení obou množin K, které jsme určili v jednotlivých větvích řešení.
U složitějších nerovnic se zpravidla už upravování nerovnice nevyhneme. Ale je nutné zachovat
ekvivalentnost všech úprav, a tak je třeba řešení rozdělit do dvou větví, jednu řešit úpravami
a druhou známou úvahou z příkladů 1 a 2.
Ukážeme si ještě jeden složitější příklad, ve kterém předvedeme několik obtížnějších případů řešení iracionálních nerovnic.
-
Příklad 4
Řešte v
nerovnici 
. -
Řešení
Zadání obsahuje pod odmocninou výraz s x a tak začneme určováním D. Musíme tedy vyřešit jednoduchou kvadratickou nerovnici:
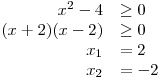
Kořeny příslušné kvadratické rovnice máme, ještě si načrtneme graf příslušné kvadratické funkce.
Aby byl výraz v zadání pod odmocninou nezáporný, musí být
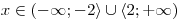.Na základě této podmínky zapíšeme O a D.
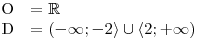
Tentokrát je výraz na levé straně nerovnice pro každou hodnotu x nekladný, zatímco výraz na pravé straně své znaménko mění. Určeme si tedy jak:
Opět tedy rozdělíme řešení této nerovnice do dvou větví:
x ≤ 2 x > 2 Definiční obor této větve řešení tedy bude: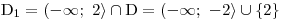 
Definiční obor této větve bude doplněk D1 do celkového D, tedy: 
Obě strany nerovnice jsou nyní nekladné, a tak je můžeme ekvivalentně umocnit na druhou. Nezapomeneme přitom otočit znaménko nerovnosti, a pak nerovnici dále upravíme.
Samozřejmě nezapomínáme otáčet znaménko nerovnosti při dělení obou stran záporným číslem.Tuto nerovnici by v oboru reálných čísel řešilo nekonečně mnoho čísel. My ale v této větvi máme dovolena používat jen
Tuto množinu získáme jako průnik D s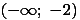 
., a proto tuto nerovnici splňuje jen číslo 2.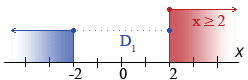
Opět v této větvi řešení máme nerovnici s opačnými znaménky na obou stranách.
Pro všechna x > 2 mají levá a pravá strana tato znaménka:
Tedy zapsaná nerovnost je splněna pro všechna x > 2, a tomu bude odpovídat i K2.
Na závěr opět sjednotíme K1 a K2 do výsledného K.
Tento příklad nám ukázal několik novinek: Předvedli jsme si umocňování obou stran nerovnice,
pokud jsou obě nekladné. Poprvé se pod odmocninou vyskytoval kvadratický výraz a tak
určování podmínek platnosti nebylo úplně triviální. Také určování K1 nebylo úplně jednoduché,
zejména si bylo třeba ve správný okamžik uvědomit, jaké hodnoty x jsou v dané větvi dovoleny.