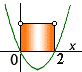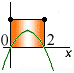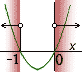Úlohy k opakování
-
Úloha 1
Řešte zpaměti v
 nerovnici
nerovnici 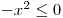 .
. -
 Jakých hodnot nabývá levá strana?
Jakých hodnot nabývá levá strana?
Levá strana nerce nabývá vždy nekladných hodnot. Pokud je x nulové, je i levá strana nulová, jinak je vždy záporná.
Hledáme, pro která x je levá strana menší nebo rovna nule, a proto
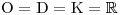 .
.

-
Úloha 2
Řešte zpaměti v
 nerovnici
nerovnici 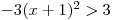 .
. -
 Jakých hodnot nabývá levá strana?
Jakých hodnot nabývá levá strana?
Levá strana nerce obsahuje součin. Záporným číslem násobím závorku umocněnou na druhou, která bude vždy nezáporná. Celá levá strana tedy bude vždy nekladná.
Na pravé straně je kladné číslo 3, a proto vždy nekladná záporná levá strana nikdy nebude větší než číslo 3.
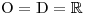
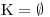
 Některé nerce (nejen kvadratické) se dají řešit bez jakéhokoliv počítání, či používání
Některé nerce (nejen kvadratické) se dají řešit bez jakéhokoliv počítání, či používání
nějakých metod, jen za pomoci logického uvažování.

-
Úloha 3
Řešte v
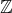 nerovnici
nerovnici 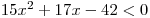 .
. -
 Určíme O, D a hodnotu koeficientů.
Určíme O, D a hodnotu koeficientů.
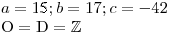
 Zkusíme určit kořeny příslušné kvadratické rce.
Zkusíme určit kořeny příslušné kvadratické rce.
Kořeny příslušné kvadratické rce jsou:
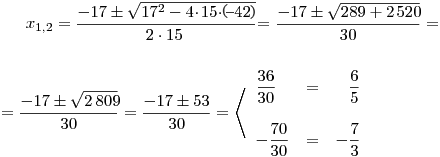
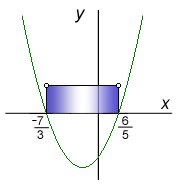
 Načrtneme graf příslušné kvadratické fce.
Načrtneme graf příslušné kvadratické fce.
Načrtneme graf příslušné kvadratické fce a vyznačíme interval, který vyhovuje zadané nerovnici.
 Určíme K.
Určíme K.
Kdybychom řešili nerovnici v
 , pak by řešením byla
, pak by řešením byla 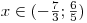 . Protože řešíme nerovnici v
. Protože řešíme nerovnici v 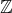 , bude
, bude 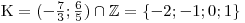 .
. Řešíme-li nerovnice v jiném O, než v
Řešíme-li nerovnice v jiném O, než v  , stačí tomuto oboru "přizpůsobit" až poslední část řešení.
, stačí tomuto oboru "přizpůsobit" až poslední část řešení.

-
Úloha 4
Řešte v
 nerovnici
nerovnici 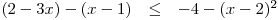 .
. -
 Určíme O, D a rovnici upravíme.
Určíme O, D a rovnici upravíme.
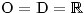
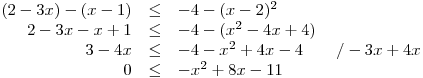
 Určíme hodnotu koeficientů a vypočteme kořeny příslušné kvadratické rce.
Určíme hodnotu koeficientů a vypočteme kořeny příslušné kvadratické rce.
a = −1; b = 8; c = −11;
Kořeny příslušné kvadratické rce jsou:
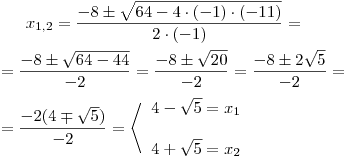
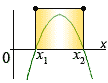
 Načrtneme graf příslušné kvadratické fce a vyznačíme v něm řešení nerce.
Načrtneme graf příslušné kvadratické fce a vyznačíme v něm řešení nerce.
Načrtneme graf příslušné kvadratické fce a vyznačíme interval, který vyhovuje zadané nerovnici.
Koeficient a < 0, proto bude parabola otevřená dolů:
 Určíme K.
Určíme K.
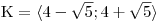
 Tato kvadratická nerovnice by vám neměla dělat příliš velké problémy. Sice jsme výrazy
Tato kvadratická nerovnice by vám neměla dělat příliš velké problémy. Sice jsme výrazy
s neznámou při úpravách nechali vpravo, museli jsme i "obrátit" význam znaménka ≤,
ale jinak byl toto příklad standardní obtížnosti.

Testíky
Klikněte na otazník u odpovědi, o které myslíte, že je dobře, a smajlík vám prozradí, zda jste odpověděli správně. U každého příkladu je jen jedna správná možnost.
|
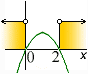
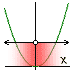
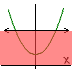
Jaký z nabízených grafů odpovídá řešení nerovnice −x2 + 2x > 0? |
||
|
|
|
|
|
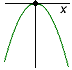
Jaký z nabízených grafů odpovídá řešení nerovnice 0 ≥ x2? |
||
|
|
|
|
|
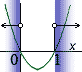
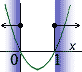
Jaký z nabízených grafů odpovídá řešení nerovnice x2 + x > 0? |
||
|
|
|
|
Řešení dalších úloh si můžete vyzkoušet v testu v kapitole za kvadratickými rovnicemi a nerovnicemi.