ROVNICE
A NEROVNICE

Grafické řešení kvadratických nerovnic

Kvadratická funkce

Pro potřeby grafického řešení kvadratické nerovnice si nejdříve vysvětlíme grafy kvadratických funkcí. Tato problematika je velmi obsáhlá, a tak se zde omezíme na naprosté minimum. Pokud by vás zajímaly podrobnosti, doporučuji navštívit diplomovou práci J. Richtera, věnovanou funkcím v rozsahu učiva střední školy.

Kvadratická funkce je dána předpisem y = ax2 + bx + c, kde a ≠ 0 . Budeme-li do předpisu této funkce za x dosazovat různá reálná čísla, můžeme pro každé z nich vypočítat příslušnou hodnotu y.

Pokud x a k němu příslušné y zapíšeme do uspořádané dvojice jako [ x ; y ], můžeme na tento zápis nahlížet jako na souřadnice bodu v rovině. Pokud do zvolené roviny s vodorovnou osou x a svislou osou y vyneseme všechny takto vypočtené body, dostaneme křivku, kterou nazveme grafem kvadratické funkce.

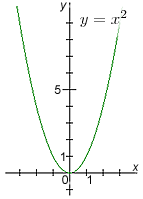
Grafem kvadratické funkce je křivka, která se jmenuje parabola. Jak parabola vypadá nám ukazují následující grafy funkcí y = x2;    y = −x2 − 1;    y = x2 − 2x − 3.

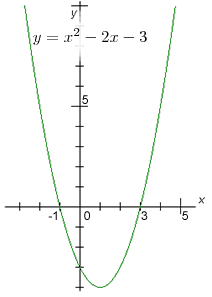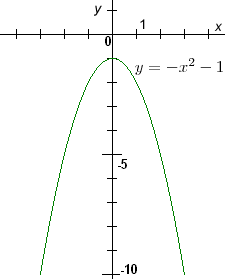
parabola otevřená nahoru parabola otevřená dolů parabola otevřená nahoru

Ještě se nám bude hodit jeden fakt. "Otevření" paraboly závisí na koeficientu u kvadratického členu a. Pro a > 0 bude grafem parabola otevřená nahoru, pro a < 0 parabola otevřená dolů. nahoru

Kvadratické funkce a kvadratické rovnice

Řešíme-li kvadratickou rovnici 0 = ax2 + bx + c, vlastně tím hledáme x-ové souřadnice bodů z grafu kvadratické funkce, jejichž souřadnice y je nulová. Neboli hledáme průsečíky grafu funkce s osou x. To se dá ilustrovat na předchozích příkladech.

Mějme funkci y = x2. Vyřešíme-li rovnici 0 = x2, dostaneme pouze jeden kořen, a to x = 0. I na ukázce grafu této funkce je vidět, že parabola osu x protíná (dotýká se osy x) pouze v bodě [ 0 ; 0 ].

U funkce y = −x2 − 1 nám diskriminant příslušné kvadratické rovnice vyjde D = 02− 4⋅(−1)⋅(−1) = −4. Tato rovnice kvůli zápornému diskriminantu nemá kořeny v a proto ani graf funkce y = −x2 − 1 neprotíná osu x.

Naopak příslušná rovnice k třetí funkci x2 − 2x − 3 = 0 se dá upravit na tvar (x + 1)(x − 3) = 0 a tedy má kořeny −1 a 3. I na grafu je vidět, že v bodech [ −1 ; 0 ] a [ 3 ; 0 ] protíná vodorovnou osu x.

nahoru

Kvadratické funkce a kvadratické nerovnice

Srovnáme-li předpisy kvadratické funkce y = ax2 + bx + c a kvadratické nerovnice ax2 + bx +c > 0, můžeme nerovnici interpretovat jako úkol: "Hledáme takové x-ové souřadnice bodů grafu [ x ; y ], aby jejich y-ová souřadnice byla větší než nula".

Neboli hledáme takové hodnoty x, pro než bod [ x ; y ] leží nad osou x.

Kdyby v nerovnici bylo jiné znaménko nerovnosti, museli bychom tento úkol přeformulovat podle daného znaménka. Pokud by nerovnice měla tvar ax2 + bx +c ≤ 0, hledali bychom takové hodnoty x, pro než bod [ x ; y ] leží pod, nebo na ose x.

Ukážeme si tedy řešení dvou kvadratických nerovnic, jejichž příslušné funkce už známe.

Řešte nerovnici x2 < 0.

Připomene si graf funkce y = x2.

Hledáme-li, kdy je x2 menší než nula, potřebujeme zjistit pro která x bude "graf funkce pod osou x".

Na první pohled je na obrázku vidět, že toto nebude splněno pro žádný bod grafu, a tedy ani pro žádné x.

Tato nerovnice má tedy .

To je ostatně poznat už ze zadání nerce. Jakékoliv reálné číslo umocněné
na druhou je vždy nezáporné, a tedy není nikdy menší než nula.

Řešte nerovnici x2 − 2x − 3 ≤ 0.

Opět si připomeneme graf funkce y = x2 − 2x − 3.

Již jsme si ukázali, že příslušná kvadratické rovnice x2 − 2x − 3 = 0 má kořeny −1 a 3, a je ostatně i vidět na grafu, že v těchto hodnotách protíná graf osu x.

Při řešení zadané nerovnice tedy hledáme takové hodnoty x, pro něž "je parabola pod osou x," nebo ji protíná.

Z grafu snadno vyčteme, že to je splněno pro , neboli .
nahoru

Postup při grafické metodě řešení

Mějme nerovnici ax2 + bx +c > 0.

  1. Určíme O a D.
  2. Vypočteme kořeny x1, x2 příslušné rovnice ax2 + bx +c = 0, existují-li.
  3. Podle koeficientu u kvadratického členu (a) určíme, zda parabola, jako graf příslušné funkce
    y =ax2 + bx +c , bude otevřená nahoru, nebo dolů.
  4. Zhruba načrtneme graf příslušné funkce. Dbáme jen na směr otevření a průsečíky s osou x.
  5. Podle znaménka nerovnosti určíme, zda nás zajímá část paraboly pod osou x ( pro znaménko <), nad osou x (pro znaménko >), pod a nebo protínající osu x (pro znaménko ≤), či nad a nebo protínající osu x (pro znaménko ≥).
  6. Určíme K
    7. .
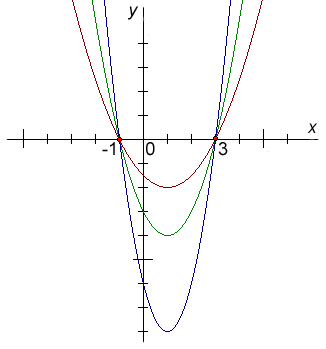
V bodě 4 nám pro řešení kvadratických nerovnic opravdu stačí přibližný náčrt grafu příslušné funkce. Obrázek vpravo nám ukazuje, že ať už parabola otevřená nahoru, protínající osu x v hodnotách −1 a 3, má jakýkoliv tvar, nemá to vliv na to, které její části jsou nad, nebo pod osou x.
nahoru

Řešené příklady

Příklad 1

Řešte v nerovnici .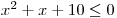

Řešení

Určíme .

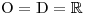Nyní budeme počítat kořeny příslušné rovnice .

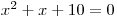Jenže 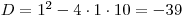, proto tato rovnice nebude mít reálné kořeny. Stejně tak graf příslušné kvadratické funkce nebude mít průsečíky s osou x. Vzhledem k tomu, že a = 1, bude grafem parabola otevřená nahoru.

Načrtneme přibližně graf:

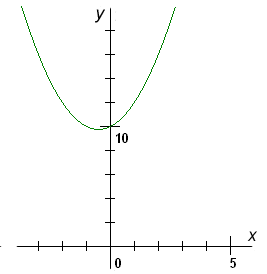
Hledáme-li, pro která x se parabola nachází pod osou x nebo protíná osu x vzhledem k danému znaménku nerovnosti, vidíme, že taková x neexistují. Tedy .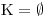

Ukazuje se, že pokud umíme grafické řešení kvadratických nerovnic,
je to poměrně rychlá a spolehlivá metoda, jak dospět k řešení.

nahoru

Příklad 2

Řešte v nerovnici .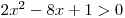

Řešení

Určíme .

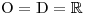Vypočteme kořeny příslušné rovnice .

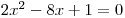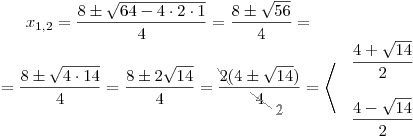
Vzhledem k a = 2 bude grafem příslušné funkce parabola otevřená nahoru:


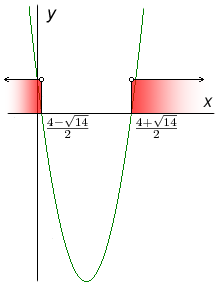
Opravdu nezáleží na přesnosti grafu, ani na umístění kořenů na osu x. Musíme si ale dát pozor, abychom menší z kořenů umístili vlevo od většího!

Hledáme, pro která x je parabola nad osou x. Podle grafu určíme, že to platí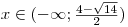 pro a pro 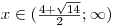. Tedy .

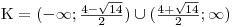Další rychlé řešení kvadratické nerovnice grafickou metodou. Kdybychom obdobnou úlohu řešili
převedením na součinový tvar a tabulkou, trvalo by nám to daleko déle.

Pro obrázky grafů kvadratických funkcí v této i následujících kapitolách, jsem využil programu pro výuku funkcí ve středoškolské matematice od Daniela Míči, který byl vytvořen jako diplomová práce na KDM MFF UK. nahoru