Úlohy k opakování
-
Úloha 1
Řešte zpaměti v
 nerovnici |-x| < 5
nerovnici |-x| < 5
-
 Neupravíme vnitřek abs. hodnoty?
Neupravíme vnitřek abs. hodnoty?
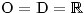
Zadaná nerovnice bude ekvivalentní s nerovnicí |x| < 5
A ta má řešení
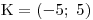 .
. Tuto nerovnici je jednoduché vyřešit, zapamatujeme-li si, že |−x| = |x|
Tuto nerovnici je jednoduché vyřešit, zapamatujeme-li si, že |−x| = |x|

-
Úloha 2
Řešte zpaměti v
 nerovnici |x + 3| ≤ 4.
nerovnici |x + 3| ≤ 4. -
 Co kdybychom nerovnici interpretovali jako požadavek ne vzdálenost obrazů čísel od −3?
Co kdybychom nerovnici interpretovali jako požadavek ne vzdálenost obrazů čísel od −3?
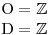
Nerovnici interpretujeme takto: vzdálenost obrazů celých čísel, která hledáme je menší nebo rovna čtyřem od obrazu −3.
Nezapomene, že rovnici řešíme jen v oboru celých čísel a tak K nebude interval, ale můžeme ho vypsat výčtem:
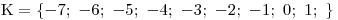
 Nezapoměňte, že rozmezí celých čísel se nedá zapsat pomocí intervalů.
Nezapoměňte, že rozmezí celých čísel se nedá zapsat pomocí intervalů.

-
Úloha 3
Řešte v
 rovnici
rovnici 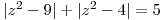 .
. -
 Určíme O, D.
Určíme O, D.
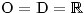
 Určíme nulové body výrazů s absolutními hodnotami.
Určíme nulové body výrazů s absolutními hodnotami.
x01 = −3, x02 = 3, x03 = −2, x04 = 2
 Sestavíme tabulku.
Sestavíme tabulku.
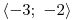
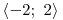
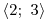
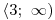
|z2 − 9| +
|z2 − 9|−
|9 − z2|−
|9 − z2|−
|9 − z2|+
|z2 − 9| Vyplníme první
Vyplníme první
řádek tabulky.|z2 − 4| +
|z2 − 4|+
|z2 − 4|−
|4 − z2|+
|z2 − 4|+
|z2 − 4| Vyplníme druhý
Vyplníme druhý
řádek tabulky. Vypočteme rovnici v prvním sloupci.
Vypočteme rovnici v prvním sloupci.
1)
 Vypočteme rovnici v druhém sloupci.
Vypočteme rovnici v druhém sloupci.
2)
 Vypočteme rovnici ve třetím sloupci.
Vypočteme rovnici ve třetím sloupci.
3)
 Vypočteme rovnici
Vypočteme rovnici
ve čtvrtém sloupci.výpočet je stejný jako v druhém sloupci, jen K4 =
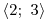
 Vypočteme rovnici
Vypočteme rovnici
v pátém sloupci.výpočet je stejný jako v prvním sloupci, jen K5 = {3}
ad 1)
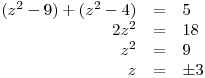
K1 = {−3}
ad 2)
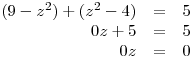
K2 =
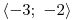
ad 3)
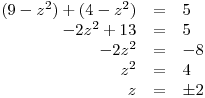
K3 = {−2; 2}
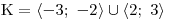
 Díky absolutním hodnotám nám najednou místo jednotlivých kořenů vyšly celé intervaly
Díky absolutním hodnotám nám najednou místo jednotlivých kořenů vyšly celé intervaly
kořenů rce. Také jsme si ukázali, že není třeba počítat rce ve všech sloupečkách. Pokud
jsou dvě stejné, stačí je upravit ke kořenům jen jednou a jen určit kořeny pro oba sloupce.

-
Úloha 4
Řešte v
 rovnici
rovnici 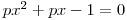 s neznámou x a parametrem p.
s neznámou x a parametrem p. -
 Určíme O, D a zapíšeme si koeficienty a, b, c.
Určíme O, D a zapíšeme si koeficienty a, b, c.
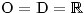
Určíme hodnotu koeficientů: a = p; b = p; c = −1
 Co když p = 0?
Co když p = 0?
Pokud p = 0, pak zadaná rovnice není kvadratická. Nemůžeme ji tedy řešit vzorečkem s diskriminantem. Dosadíme tedy za p číslo 0:
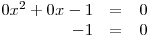
Vidíme, že pro p = 0 nemá rovnice žádné řešení.
 Když p ≠ 0, tak vypočítáme kořeny.
Když p ≠ 0, tak vypočítáme kořeny.
Pro p ≠ 0:
Dosadíme hodnoty koeficientů do vzorečku pro výpočet kořenů.
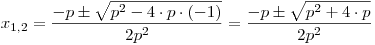
 Určíme znaménko diskriminantu.
Určíme znaménko diskriminantu.
D = p2 + 4p
Abychom určili, kdy bude diskriminant kladný, vyřešíme kvadratickou nerovnici p2 + 4p > 0.
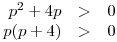
Kořeny příslušné kvadratické rovnice jsou p1 = 0, p2 = −4. Nyní načrtneme graf příslušné kvadratické funkce a vyznačíme řešení.
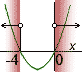
Diskriminant tedy bude kladný pro
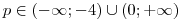 .
. Určíme řešení pro různé hodnoty p.
Určíme řešení pro různé hodnoty p.
Pro p ∈ (−4; 0) je D záporný a rovnice nemá žádné řešení.
Pro p = −4
 Případ, když p = 0, jsme už vyřešili výše. je diskriminant nulový a rovnice má jeden dvojnásobný kořen:
Případ, když p = 0, jsme už vyřešili výše. je diskriminant nulový a rovnice má jeden dvojnásobný kořen: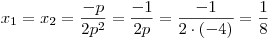
Pro
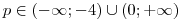 má rovnice 2 kořeny:
má rovnice 2 kořeny: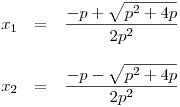
 Sestavíme závěrečné schéma.
Sestavíme závěrečné schéma.
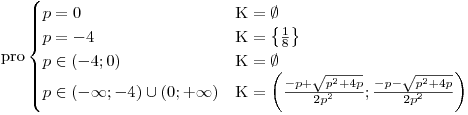
 V této kvadratické rci jsme museli řešit ještě vedlejší nerci, abychom určili znaménko
V této kvadratické rci jsme museli řešit ještě vedlejší nerci, abychom určili znaménko
diskriminantu. Je důležité se pak vždy vrátit k řešení původního příkladu a neskončit v půlce.
