Parametry v matematice
Se slovem parametr se setkáváme i v běžném životě poměrně často. Hovoříme o parametrech různých strojů a nástrojů, čímž máme na mysli jejich různé charakteristiky jako výkon, hmotnost apod.
V matematice slovo parametr nejčastěji znamená nějaké číslo, jehož konkrétní hodnotu v době řešení, nebo zpracování úlohy ještě neznáme. Nicméně potřebujeme onu úlohu vyřešit i bez této znalosti, abychom pak mohli pro konkrétní hodnoty parametrů jednoduše získat konkrétní řešení celé úlohy.
Kromě rovnic se s parametry potkáváme zejména v analytické geometrii, kdy se pomocí parametrů zadávají předpisy křivek a ploch. O tomto se více můžete dozvědět v Odvárko a kol. [7].
Řešení rovnic s parametry
Výrazy na obou stranách rovnic s parametry mohou obsahovat více symbolů - písmen. Je nutné, abychom se v zadání dozvěděli, která ze symbolů označuje neznámou a který parametr. Dále také jakých hodnot mohou nabývat.
- Řešit rovnici s neznámou x a s parametrem t
- znamená řešit celý systém rovnic, tj. ke každé přípustné hodnotě parametru t určit obor pravdivosti K rovnice, kterou získáme po dosazení této hodnoty za t.
Řešení rovnic s parametry je velmi různorodé. Na střední škole se standardně nepotkáme s těžšími rovnicemi, než jsou kvadratické rovnice s dvěma parametry, ale i některé takovéto příklady mohou být značně obtížné. Je proto nezbytně nutné perfektně ovládat řešení rovnic bez parametru, jak lineárních, tak kvadratických.
Řešené příklady
-
Příklad 1
Řešte v
rovnici
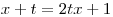s neznámou x a reálným parametrem t. -
Řešení
Není vždy snadné v rovnici s parametrem určit D, ale v tomto příkladě je to jednoduché:
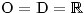.Ke všem parametrům v rovnicích přistupujeme obdobně jako ke konkrétním číslům. Tedy i v této rovnici osamostatníme na levé straně všechny výrazy s neznámou x a na straně pravé výrazy bez ní.
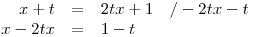
Výrazy na levé straně už nejde "více sečíst". Ale oba dva obsahují v první mocnině neznámou x, kterou z obou vytkneme.
Nyní bychom potřebovali obě strany rovnice vydělit výrazem 1 − 2t. To ale nemůžeme udělat, protože by tento výraz mohl být nulový, a pak bychom neprováděli ekvivalentní úpravu. Musíme řešení celé rovnice rozdělit do dvou větví - v jedné bude pro parametr platit 1 − 2t = 0 a ve druhé nikoliv.
V této větvi výpočtu pro parametr t platí:
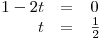
Počítáme-li řešení rovnice pro konkrétní hodnotu parametru, pak můžeme do rovnice tuto hodnotu dosadit a vyřešit klasickou rovnici:
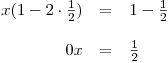
Z toho určíme, že pro
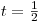nemá rovnice žádné řešení, a tedy K1 = ∅.
V této větvi je
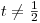
Obě strany rovnice
tedy můžeme vydělit nenulovým výrazem 1 − 2t.Dostaneme:
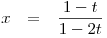
Tedy pro
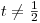je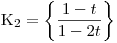 
.
Na závěr vytvoříme schéma, ve kterém shrneme určená K pro jednotlivé hodnoty parametru t:
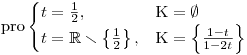
Nezapomeňte, že i když s parametry pracujeme jako s čísly, neznáme přesně jejich hodnotu,
a často ani jejich znaménko. Proto, kdykoliv pro další krok ve výpočtu budeme tuto znalost potřebovat,
budeme muset výpočet větvit. Důležité je i správně zapsat výsledné K, kde musí být určena
množina všech kořenů pro všechny přípustné hodnoty parametru.
-
Příklad 2
Řešte v
rovnici
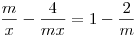s neznámou x a s reálným parametrem m. -
Řešení
Nejprve určíme O a D.
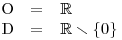
Měli bychom si ale všimnout, že ani pro m = 0 nebudou výrazy na obou stranách rovnice definovány. Proto celou rovnici dále budeme řešit pro m ≠ 0.
Nejprve rovnici upravíme:
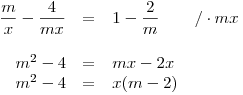
Nyní potřebujeme rovnici dělit výrazem m −2 , proto musíme opět výpočet rozdělit do dvou větví.
Je-li m = 2 pak platí:
Známe konkrétní hodnotu parametru m, a tak ji dosadíme:
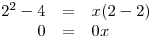
Této rovnici vyhovují tedy všechna x z definičního oboru D, tj.
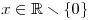.Je-li m ≠ 2, pak platí:
Obě strany rovnice můžeme vydělit nenulovým výrazem m − 2:
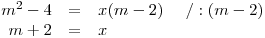
Parametr m může v této větvi nabývat všech reálných čísel až na 0 a 2.
Pro m = −2 by x = 0, což je zakázáno definičním oborem, a tedy pro m = −2 tato rovnice nemá mít žádné řešení.
A nyní všechny získané poznatky v závěru shrneme podle závislosti řešení rovnice na hodnotě parametru m:
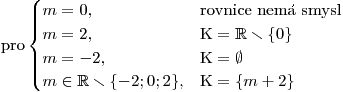
Během řešení rovnic s parametry je třeba neustále kontrolovat, zda všechny zápisy vyhovují
všem výše napsaným podmínkám. Kdybychom to nedělali, nevšimli bychom si, že pro m = −2
nemá tato rovnice řešení.
-
Příklad 3
Řešte v
rovnici
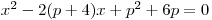s neznámou x a s reálným parametrem p. -
Řešení
Tentokrát je určení O a D jednoduché:
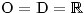
Toto je kvadratická rovnice s parametrem. Budeme ji řešit pomocí vzorečku s diskriminantem, takže si určíme koeficienty a,b,c.
a = 1; b = −2(p + 4); c = p2 + 6p
Tyto koeficienty teď dosadíme do vzorečku pro výpočet kořenů:
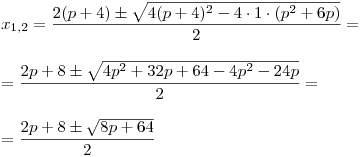
Po úpravách jsme zjistili, že diskriminant D = 8p + 64. Na základě tohoto výrazu nyní určíme zda existují kořeny a které to jsou.
Pro určení podmínky, kdy je D = 0, vypočteme:
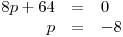
Je-li p = −8, pak má kvadratická rovnice jeden kořen:
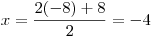
Bude-li p < −8, pak je diskriminant D záporný a celá rovnice nemá žádný kořen v oboru reálných čísel.
Pro p > −8 určíme nyní kořeny:
Výše uvedené poznatky teď už jen shrneme do závěrečního schématu:
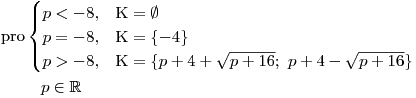
Jak jsme si několikrát ukázali, parametr nemusí ovlivňovat jen hodnotu kořenů, ale i jejich
počet. Zde se to projevilo v různých hodnotách diskriminantu kvadratické rovnice.