Řešení nerovnic s parametry
Stejně jako rovnice s parametry, existují i nerovnice s parametry. Jejich řešení není principiálně jiné než řešení rovnic s parametry. Často ale řešení bývá rozvětveno do více částí, těžší na diskuzi řešení v závislosti na hodnotě parametrů a celkově náročnější na pozornost.
V této kapitole si ukážeme řešení několika příkladů, ale rozhodně neobsáhneme všechny typy, se kterými se můžete potkat během studia na střední škole. Zajímají-li vás nerovnice s parametrem více, můžete další řešené příklady najít třeba v učebnici pro gymnázia Charvát a kol. [3].
Řešené příklady
-
Příklad 1
Řešte v
nerovnici
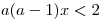s neznámou x a reálným parametrem a. -
Řešení
I tentokrát je určení D jednoduché:
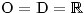.Zadanou lineární nerovnici bychom rádi řešili osamostatněním x na levé straně nerovnice. Nemůžeme ale obě strany nerovnice vydělit výrazem a(a − 1), protože ten by mohl být nulový. Rozdělíme tedy řešení do dvou větví:
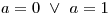
a tedy výraz a(a − 1) je nulový.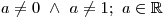
a tedy výraz a(a − 1) je nenulový.Rovnici můžeme dosazením upravit na tvar:
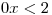.Snadno pak určíme, že takovou nerovnici řeší všechna
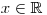.Můžeme tedy výrazem a(a − 1) vydělit obě strany nerovnice. Jenže tento výraz může nabývat kladných i záporných hodnot a nevíme zda při dělení otáčet či neotáčet znaménko nerovnosti.
Nejprve si určíme, pro jaké hodnoty a nabývá výraz kladných hodnot. Vyřešíme tedy kvadratickou nerovnici
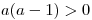.Kořeny příslušné kvadratické rovnice jsou a1 = 0 a a2 = 1.
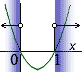
Z grafu příslušné kvadratické funkce pak vyčteme pro která a bude
.
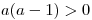Pro
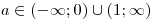je výraz a(a − 1) kladný a při úpravě původní nerovnice nemusíme otáčet znaménko nerovnosti.
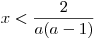
Pro
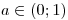je výraz a(a − 1) záporný a tudíž při dělení obou stran původní nerovnice tímto výrazem, otočíme znaménko nerovnosti, abychom zachovali ekvivalentnost úprav.
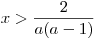
Na závěr vytvoříme schéma, ve kterém zapíšeme K pro jednotlivé hodnoty parametru a.
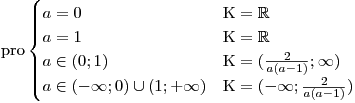
Oproti rcím s parametry se v nercích komplikují i úpravy, kdy chceme obě strany nerce
vynásobit (příp. vydělit) výrazem s parametrem. Není-li na první pohled jasné znaménko
tohoto výrazu, musíme řešit další nerci, abychom jej určili a rozdělit podle něj řešení.
-
Příklad 2
Řešte v
nerovnici
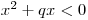s neznámou x a s reálným parametrem q. -
Řešení
Určení O a D bude zase jednoduché:
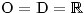.Toto je kvadratická nerovnice s parametrem. Kvadratickou nerovnici budeme řešit grafickou metodou, a budeme sledovat, jak toto řešení ovlivní parametr q.
Určíme si koeficienty kvadratické nerovnice:
a = 1; b = q; c = 0
Nyní vypočteme kořeny příslušné kvadratické rovnice.
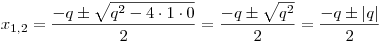
Ve výpočtu kořenů se objevil výraz |q|. Pokud bychom jej chtěli nahradit výrazem bez absolutní hodnoty, museli bychom rozdělit další řešení do tří větví:
Pro q > 0 můžeme místo |q| počítat jen s q. Pro q = 0 můžeme tuto hodnotu dosadit. Pro q < 0, můžeme |q| nahradit výrazem −q.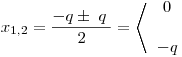 
Známe kořeny a můžeme si načrtnout graf, ze kterého určíme řešení zadané nerovnice
.
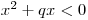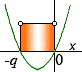
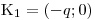
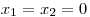
Na základě vypočteného dvojnásobného kořenu načrtneme graf příslušné kvadratické funkce a určíme řešení nerovnice
.
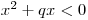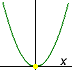
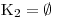
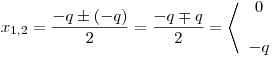
Načrtneme si graf příslušné kvadratické funkce a určíme z něj řešení nerovnice
. 
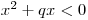Uvědomte si, že pokud q < 0 pak výraz −q je kladné číslo.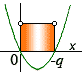
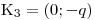
Nakonec shrneme závislost řešení nerovnice na hodnotě parametru q.
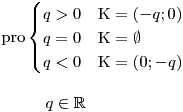
Při řešení téměř každé kvadratické rovnice (nerovnice) s parametrem nastane situace,
kdy musíme posoudit, zda znaménko diskriminantu D závisí na hodnotě parametru, či nikoliv.
Tentokrát byl D = q2 vždy nezáporný, proto jsme řešení dělili do tří větví až při výpočtu kořenů,
abychom mohli odhadnout polohu průsečíků grafu příslušné kvadratické funkce s osoux.